Heisenberg exchange coupling of iron and cobalt¶
Version: S-2021.06
In this tutorial you will learn how to use the HeisenbergExchange analysis object to calculate the Heisenberg exchange coupling parameters of bulk Fe and Co. You will also learn how to calculate the Curie temperature and exchange stiffness from the coupling parameters.

Introduction¶
When studying magnetic properties of materials, density functional theory (DFT) often provides a good description. From the spin-density it is possible to calculate the zero-temperature magnetization and magnetic ordering and one can calculate the exchange splitting from the bandstructure or density of states. It is, however not a standard analysis to calculate excited state properties such as the exchange stiffness, Curie temperature, spin wave dispersions, or magnetization dynamics.
When studying such quantities the starting point is often the Heisenberg model. The Heisenberg exchange Hamiltonian is given by [1], [2]
where \(\hat{e}_i\) is the normalized local spin vector on atom \(i\), and \(J_{ij}\) is the Heisenberg exchange coupling constant. In the following short Theory section we will detail how the exchange coupling matrix elements are calculated from DFT calculations and we will also show how to obtain the Curie temperature and exchange stiffness.
Theory¶
We calculate the exchange coupling matrix elements \(J_{i\mathbf{0}, j\mathbf{R}}\) between an atom \(i\) in the central unit cell labeled \(\mathbf{0}\) and atom \(j\) in a different unit cell displaced from the central one with a lattice vector \(\mathbf{R}\). We use a real-space Green’s function implementation [3], [4] of the original Liechtenstein-Katsnelson-Antropov-Gubanov (LKAG) formula [1]:
where \(i\) and \(j\) label atomic indices within a unit cell, \(\mathbf{R}\) is a lattice vector, and where \(\Delta_i = H_i^\uparrow - H_i^\downarrow\) is the on-site difference between the up and down part of the Hamiltonian matrix. More details about the implementation can be found in the reference manual Notes.
Curie temperature¶
The Curie temperature, \(T_C\), of a ferromagnet is the temperature at which the average magnetic moment becomes zero due to random fluctuations of the local magnetic moment directions. \(T_C\) can be estimated from the Heisenberg model in different ways. Within the mean field approximation (MFA) one have [2]
The MFA formula typically overestimates the Curie temperature when compared to experiments as will also be evident below. A different approach is based on the random phase approximation (RPA) [2]:
where \(E(\mathbf{q})\) is the spin wave energy at q-point \(\mathbf{q}\) and \(M\) is the magnetic moment per atom and \(\mu_B\) is the Bohr magneton. Since an average over the Brillouin zone is performed, the RPA calculation needs to be converged with respect to the number of q-points. This will be illustrated below.
Exchange stiffness¶
The exchange stiffness describes the energy of a long wavelength spin wave excitation. In particular, if the energy as function of wave number \(q\) is written as
the exchange stiffness constant, \(A_{ex}\) is seen to be given by the curvature of the \(E(q)\) vs. \(q\) curve. \(A_{ex}\) can be calculated from the Heisenberg exchange parameters as [2]:
where \(r_{i\mathbf{0}, j\mathbf{R}}\) is the distance between atom \(i\) in cell \(\mathbf{0}\) and atom \(j\) in cell \(\mathbf{R}\). In practice, (6) can be difficult to converge with respect to the sum over lattice vectors \(\mathbf{R}\). This is particularly pronounced in the case of iron where the exchange parameters are very long ranged. In this case it is possible to dampen the oscillations and extrapolate the result to zero damping as:
Below we will see how to perform the extrapolation to \(\eta \rightarrow 0\) in practice.
Setting up calculations¶
We are now ready to start calculating the Heisenberg exchange parameters for Fe and Co. In order to enable a direct comparison to ref. [2] we will be studying Co in the FCC phase. We will start by performing calculations and analysis for Co(FCC). The calculations for Fe (BCC) are performed in the same way, but the analysis, and in particular the calculation of the exchange stiffness, will require a special treatment in the case of Fe.
Open the Builder and add Cobalt (alpha) from the crystals database. Send the configuration to the Script Generator.
Now do the following:
Add an
 LCAOCalculator to the script, open the LCAOCalculator widget and apply the changes on the main page (see image below)
LCAOCalculator to the script, open the LCAOCalculator widget and apply the changes on the main page (see image below)Close the LCAOCalculator widget.
Add a
 HeisenbergExchange analysis object to the script and open the HeisenbergExchange widget. Apply the changes (see image below)
HeisenbergExchange analysis object to the script and open the HeisenbergExchange widget. Apply the changes (see image below)Change exchange interaction range to \(n_A = 9\), \(n_B = 9\), \(n_C = 9\).
Note
The exchange interaction range determines how many times the input configuration is repeated when performing summations over \(\mathbf{R}\) in the formula above. An exchange interaction range of \(n_A = 9\) means that translations corresponding to \(-5 R_A, -4 R_A, \dots 4 R_A, 5 R_A\) are included, where \(R_A\) is the lattice vector in the A-direction. Therefore, the exchange interaction range needs to be an odd integer.
Increase the k-point density to 12 (select from the Preset Densities). The k-point density determines how many k-points are used when calculating the real-space Green’s function (See (19) in the reference manual Notes).
You may also check the box Precalculate eigenstates. By checking this box, the calculation will run faster. This should however only be used for configurations with relatively few atoms as the memory requirements will be increased.

Close the HeisenbergExchange widget.
Finally change the name of the Results file to
Co-FCC.hdf5and run the calculation.
Note
The calculations are here performed using the experimental lattice constants. For more complicated structures like interfaces, a structural relaxation should be performed before the HeisenbergExchange calculation.
Analyzing the results¶
When the calculation has finished we are ready to analyze the results. Since no dedicated HeisenbergExchange analyzer has been developed yet, the analysis will be based on python scripts.
Exchange coupling element vs. distance¶
First, we will look at the exchange interactions elements themselves and make a plot of \(J_{i\mathbf{0}, j\mathbf{R}}\) vs. \(r_{i\mathbf{0}, j\mathbf{R}}\). The script plot_Jij_vs_r.py loads the just calculated HeisenbergExchange object and extracts the relevant data and plots the result. Together with the QuantumATK data we plot the data from ref. [2] for Co-FCC. Download and run the script plot_Jij_vs_r.py.
Now run the script. The script will produce a figure like the image shown below. Note that in order to make a direct comparison to the numbers from ref. [2] (Table I) we plot the exchange coupling values in units of mRy.
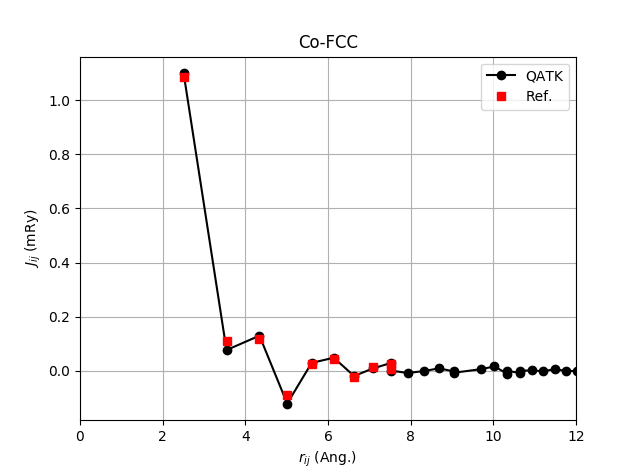
The positive sign of the nearest neighbor coupling elements shows that Co is a ferro-magnet. Due to the minus-sign in (2) the energy is lowered for aligned spins, when the coupling elements are positive leading to ferromagnetic coupling.
Note
There is no clear consensus in the literature about the sign-convention in (2) and sometimes the minus-sign is omitted.
Curie temperature¶
We now turn to the calculation of the Curie temperature. As mentioned above, there are two approximations included in QuantumATK. The mean-field approximation (MFA) formula is the most simple and the result is simply obtained:
T_C_mfa-tutorial = heisenberg_exchange.curieTemperature()
The random phase approximation includes a sum over q-points, and convergence with respect to the number of q-points should be checked. The default value might not be high enough for all cases. In the case of Co, it turns out the RPA calculated Curie temperature scales linearly with the inverse number of q-points in each direction. By performing a linear fit, it is therefor possible to extrapolate the result to the limit of infinitely many q-points by evaluating the fit \(1/n_q=0\). This is done in the script curie_temperature.py, which both calculates the MFA result and the RPA result extrapolated to infinite q-point sampling. Download and run curie_temperature.py. The output of the script is
-------------------------------------------------
Curie temperature:
-------------------------------------------------
MFA : 1648.9 K
RPA (default q-grid) : 1435.0 K
RPA (extrapolate to infinite q-grid) : 1301.1 K
-------------------------------------------------
The figure below is made by the script and illustrates the linear scaling of the RPA Curie temperature as a function of the inverse number of q-points.

The experimentally determined Curie temperature for Co is 1388-1398 K [2]. It is evident that the RPA result is in reasonable agreement with the experimental value, while the MFA clearly overestimates the Curie temperature.
Exchange stiffness¶
We will now see how to calculate the exchange stiffness for Co. The exchange stiffness given by (6) is obtained as
exchange_stiffness = heisenberg_exchange.exchangeStiffness()
As discussed above and in Ref. [2] it is sometimes necessary to dampen the long-range interaction and subsequently extrapolate to zero dampening following (7). The procedure for doing so is
extrapolated_exchange_stiffness, exchange_stiffness_vec, damping_factor_range, p_fit \
= heisenberg_exchange.extrapolatedExchangeStiffness()
where the final extrapolated result is given by extrapolated_exchange_stiffness. The other returned quantities are a vector of calculated exchange stiffness values obtained for the damping factors given by damping_factor_range. The damping_factor_range is by default determined automatically as ranging from \(0.1/d_0\) to \(1/d_0\), where \(d_0\) is the nearest neighbour distance. Finally the polynomial fit is also returned. Together, these allow for a visual inspection of the fitting and extrapolation as done in the script exchange_stiffness.py and shown in the figure below.
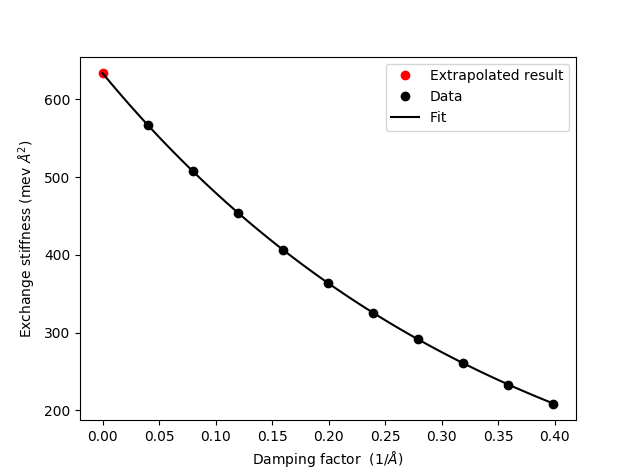
Download and run the exchange_stiffness.py. The output of the script is
-------------------------------------------------
Exchange stiffness:
-------------------------------------------------
A_ex : 633.8 meV*Ang**2
A_ex (extrapolated) : 633.7 meV*Ang**2
-------------------------------------------------
It is evident that both the direct evaluation using (6) and the extrapolated results are in close agreement. While this is often the case, the situation for Fe is a bit more complicated.
Exchange stiffness for Fe¶
We will now study the Heisenberg exchange of Fe in the BCC phase. Find Iron (alpha) in the crystal database in the Builder and repeat the steps above for calculating the  HeisenbergExchange. When modifying the HeisenbergExchange object we need to include a longer interaction range:
HeisenbergExchange. When modifying the HeisenbergExchange object we need to include a longer interaction range:
Open the HeisenbergExchange widget and change exchange the interaction range to \(n_A = 13\), \(n_B = 13\), \(n_C = 13\).
The other settings used for Co can be applied for Fe as well.
Finally change the name of the Results file to
Fe-BCC.hdf5and run the calculation.
When the calculation is done the exchange stiffness can be analyzed with the script exchange_stiffness_Fe.py. Download and run the script to get the output
-------------------------------------------------------
Exchange stiffness:
-------------------------------------------------------
A_ex : 290.7 meV*Ang**2
A_ex (extrapolated, default) : 283.7 meV*Ang**2
A_ex (extrapolated, 4th order fit : 277.2 meV*Ang**2
A_ex (extrapolated, custom range) : 270.2 meV*Ang**2
-------------------------------------------------------
and the figure
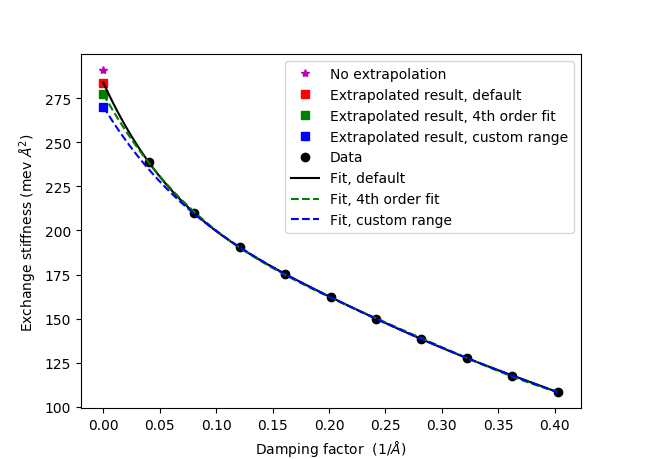
The script shows how to customize the extrapolation of the exchange stiffness by either (i) changing the polynomial order from the default value of 5 to 4, or (ii) by customizing the damping factor range. All fits look perfectly reasonable, but the extrapolated exchange stiffness constants differ somewhat. This illustrates that in the case of Fe it is difficult to define an exactly calculated exchange stiffness. More discussion on this topic can be found in Ref. [2].
Summary of results¶
The tables below summarizes the Curie temperature and exchange stiffness results and compares with calculated and experimental values from Ref. [1] = [2]. The values of extrapolated exchange stiffness are obtained using the default settings.
Curie temperatures (K) |
|||
|---|---|---|---|
QATK |
Calc. [1] |
Exp. [1] |
|
Co, MFA |
1648 |
1645 |
1388-1398 |
Co, RPA |
1301 |
1311 |
1388-1398 |
Fe, MFA |
1353 |
1414 |
1044 |
Fe, RPA |
894 |
950 |
1044 |
Exchange stiffness (meV Å^2) |
|||
|---|---|---|---|
QATK |
Calc. [1] |
Exp. [1] |
|
Co |
634 |
663 |
580 |
Fe |
284 |
250 |
280 |
It is evident that the Curie temperature results from QuantumATK matches well with the calculated results from [2]. It is also evident that the MFA overestimates the Curie temperature quite significantly compared to experiments whereas the RPA results (extrapolated to infinite q-point sampling) are significantly closer to the experimental values.
The exchange stiffness values are also in good agree with both reference calculations and experimental values.
In summary, this tutorial shows how to calculate the Heisenberg exchange coupling parameters of iron and cobalt. It is demonstrated how to calculate the Curie temperature and exchange stiffness and the obtained values are compare favorably with theoretical- and experimental results from the literature.
COSMICS project¶
The HeisenbergExchange analysis object has been developed within the project COSMICS founded by the European Union’s Horizon 2020 research and innovation program under Grant Agreement No. 766726. Details about the object can be found here HeisenbergExchange.
More information about the COSMICS project can be found here: http://cosmics-h2020.eu/

