Calculating and using Dynamical Matrix¶
Version: U-2022.12
The DynamicalMatrix is an object that is used to calculate many properties related to dynamics of the crystal lattice
e.g Mobility, RamanSpectrum, DeformationPotential, DielectricTensor and more.
In this tutorial you will learn how to calculate the dynamical matrix and use it to perform a PhononBandstructure calculation.
In particular, you will learn how to set up the calculation and which parameters are critical.
You will also learn how to optimize the performance of this type of calculations by an optimal parallelization strategy.
You will first perform a DFT-LCAO calculation with the LDA exchange-correlation functional. You will go through all the relevant parameters used in a phonon calculation.
Towards the end, you will use the classical potentials available in the ForceFieldCalculator and compare the results.
Prerequisites¶
This tutorial is an introduction to the Dynamical Matrix functionality in QuantumATK and only requires basic familiarity with the QuantumATK interface. This can be achieved via the following basic tutorials and guides:
Create the Workflow¶
Go to the 
Builder and import the Silicon (alpha) structure from the built-in database. Then send the structure to the 
Workflow Builder and add the following script blocks:
LCAOCalculator
OptimizeGeometry
DynamicalMatrix
PhononBandstructure
The resulting workflow should look like this:
Now we will go through the settings of each block and edit the important parameters.
LCAOCalculator Settings¶
To get good results for the dynamical matrix one has to converge the computational settings with respect to a few key parameters:
Note
In this example we use the light weight Single Zeta Polarized basis set. This basis set will result in a decent phononbandstructure at low computational cost. For production simulations we would recommend using e.g. the default PseudoDojo-Medium basis set which is generally more accurate.
Please also note that the Density mesh cutoff needed is material and pseudo potential specific, so while 50 Hartree is enough for SIlicon, it is too low for other materials. Generally one should start from the default value and increase until convergence is reached.
In the Workflow Builder do the following:
Open the
In the
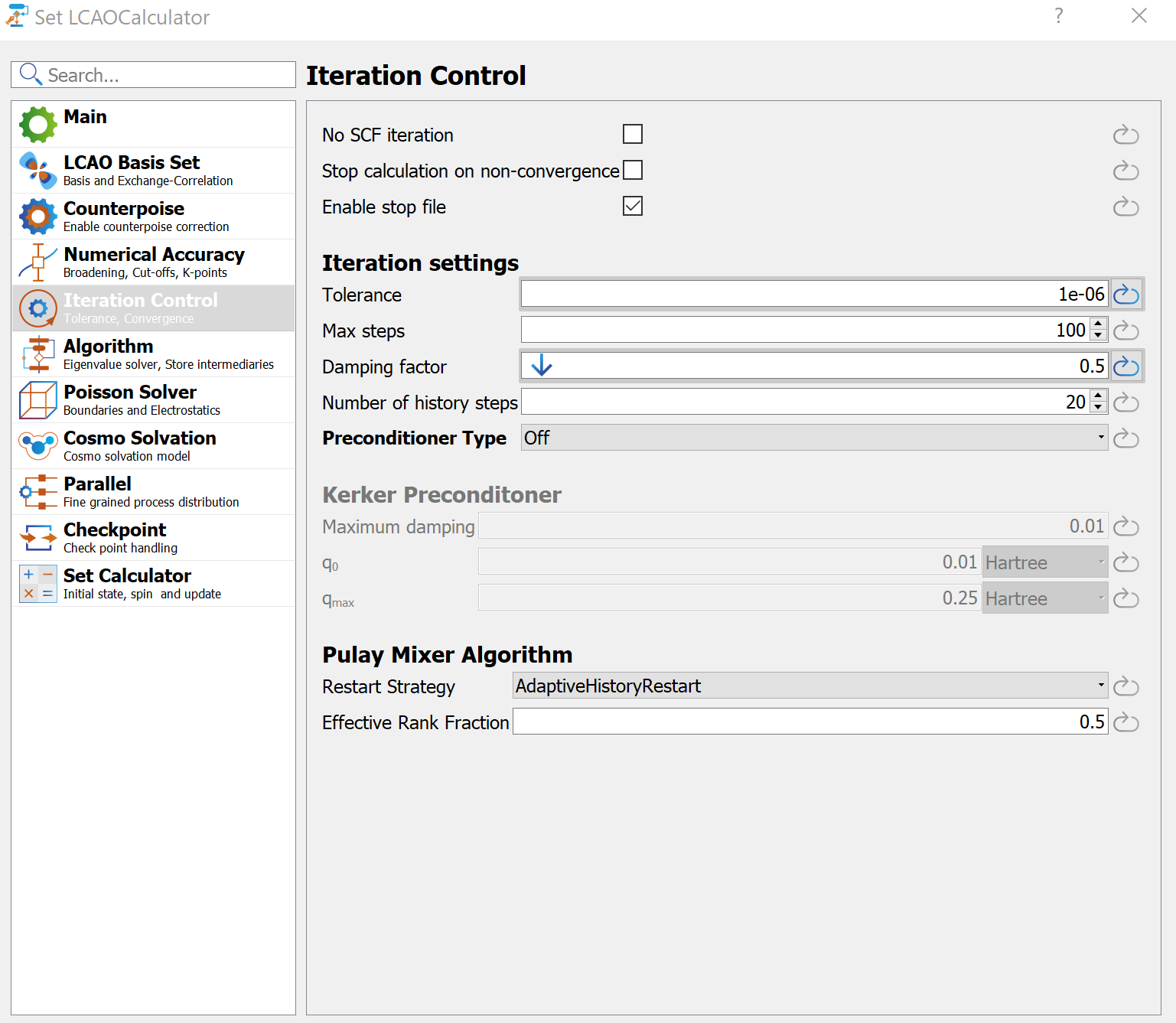
Main section, in Basic Parameters select LDA under Family, FHI under Pseudopotential and SingleZetaPolarized under Basis Set.
In the
In the
Iteration Control section, set a Damping factor of 0.5. Also reduce the Tolerance to 0.000001.
Tip
It can often be necessary to increase mesh cutoff and k-point density from the default values for DynamicalMatrix calculations to ensure convergence of the phonon bandstructure.
For non-metals in general we recommend using 300 Kelvin broadening.
For DynamicalMatrix calculations it is generally recommended to use a tighter tolerance than the default one.
It is possible to reduce the number of iteration steps by tuning the damping factor and number of history steps used.
Lattice optimization Settings¶
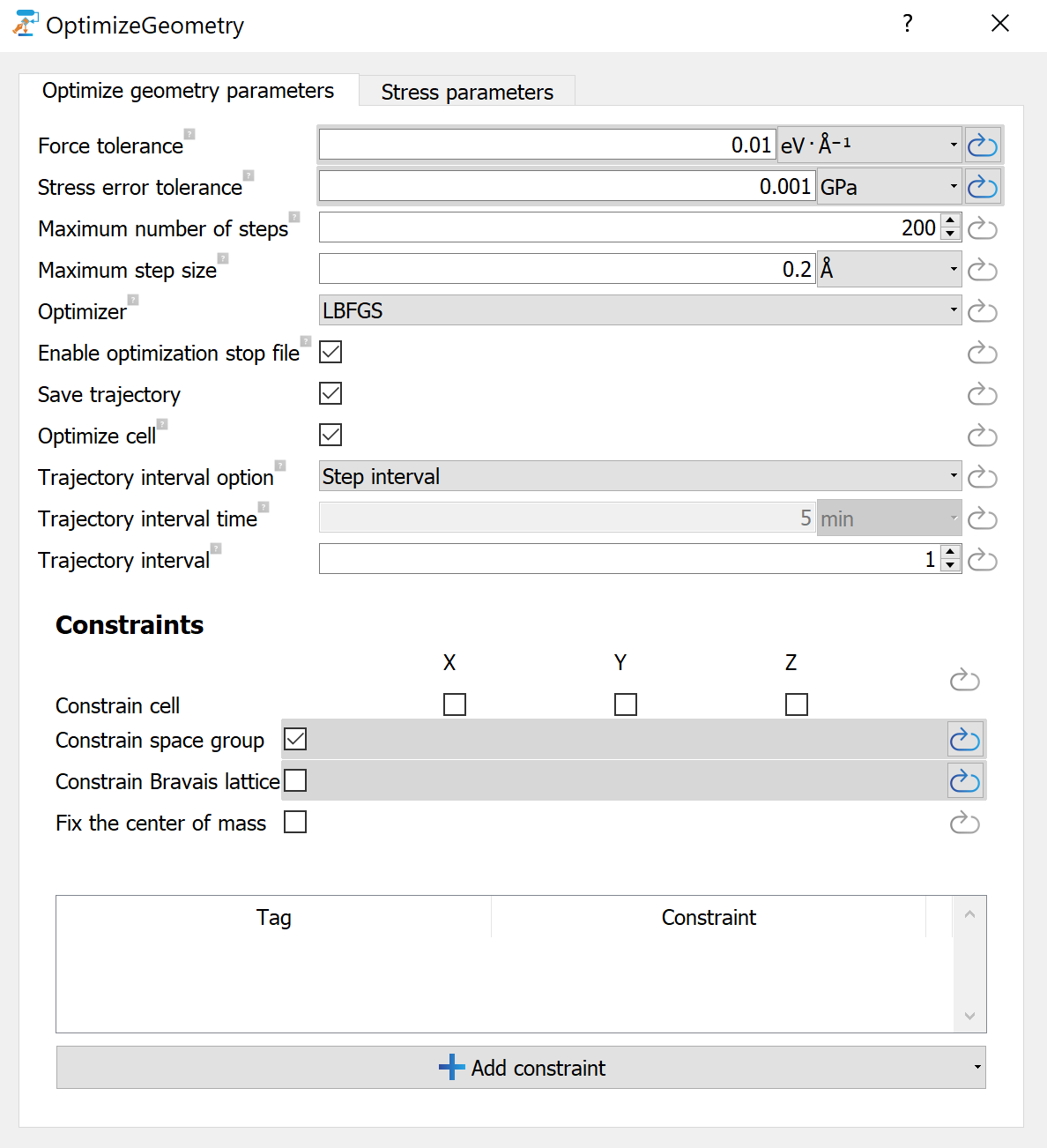
Open the OptimizeGeometry block, and modify the parameters as in the figure below
to perform a force and stress minimization with tighter-than-default convergence parameters.
Tip
We generally recommend reducing the target stress and forces when calculating the dynamical matrix.
To get good structures for calculations of electronic properties the default settings are usually sufficient.
Dynamical matrix Settings¶
The dynamical matrix is the second derivative of the energy, corresponding to the first derivative of the forces. The first derivative of the forces are calculated using a finite difference scheme, where each symmetrically unique atom in the central cell is displaced along all cartesian directions, also called frozen phonon calculations.
For crystals with small unit cells, a periodically repeated super-cell of the
unit cell is often needed to accurately account for long-range interactions in
the dynamical matrix. QuantumATK can handle this automatically. By default
cell is repeated such that all atoms within a pre-defined element-dependent
distance from the atoms in the unit cell are included in the repeated cell.
This is enough for most systems.
It is also possible to directly set the number of repetitions used in each
direction.
You can see more details in the Notes section of the manual entry for DynamicalMatrix.
In the
Open the
Note
The TAT of the calculation is highly sensitive on the number of repetitions for the simple fact that the repeated system can become very large. For highly complex or large systems where the automatically detected repetitions result in a very high TAT one can sometimes reduce the number of repetitions. It is however important for production calculations to always check convergence with respect to e.g. phononbandstructure.
To test the effect of using different numbers of repetitions, we repeat the calculation
setting Repetitions to 3x3x3 and 5x5x5. The full workflow can be downloaded here Silicon_phonon_bandstructure.hdf5.
To change the repetitions set Repetitions to Custom and choose the desired numbers.
Running the calculation¶
You are now ready to run your DFT phonon bandstructure calculation. This can be done by sending the script to the Job Manager
using the Send To icon 
.
However, there are a couple of details to consider before running the job:
Parallelization
In QuantumATK, the dynamical matrix can be calculated by parallelizing over displacements. The number of displacements needed depends on the system and can be calculated by opening the Dynamical Matrix object and pressing the Calculate… button under Number of Displacements.
The amount of processes reserved for each displacement can be controlled using the Processes per displacement parameter. In general we recommend one of two parallelization strategies:
The default setting ProcessesPerNode divides the the displacements across nodes. When running on a single node this will result in all displacements being calculated in serial.
Depending on the system considered and the hardware setup it is sometimes advantageous to run all displacements in parallel on as many processes as possible. For that strategy one should take the total number of processes subtract one which will be reserved as a delegator and then evenly distribute the remaining processes on the number of displacements.
For this tutorial, we will use the default ProcessesPerNode setting on a single 20 core node.
System size
The three systems run in this tutorial, 3x3x3, 5x5x5 and 7x7x7 repetitions, consists of 54, 250 and 686 Silicon atoms, respectively. Besides the running time you should also consider the amount of memory required.
Timing
The table below reports the total time required to run the entire phonon bandstructure workflow with the parameters set above. The calculations are run in parallel with 20 MPI processes:
Repetition |
3x3x3 |
5x5x5 |
7x7x7 |
|---|---|---|---|
Total time |
1m29s |
22m26s |
1h39m44s |
Analyzing the results¶
When the job is done you will find in the 
Data view the PhononBandStructure object.
Highlight it and press 
Open to display it.
The figure below reports results for the 3x3x3, 5x5x5 and 7x7x7 systems defined above.
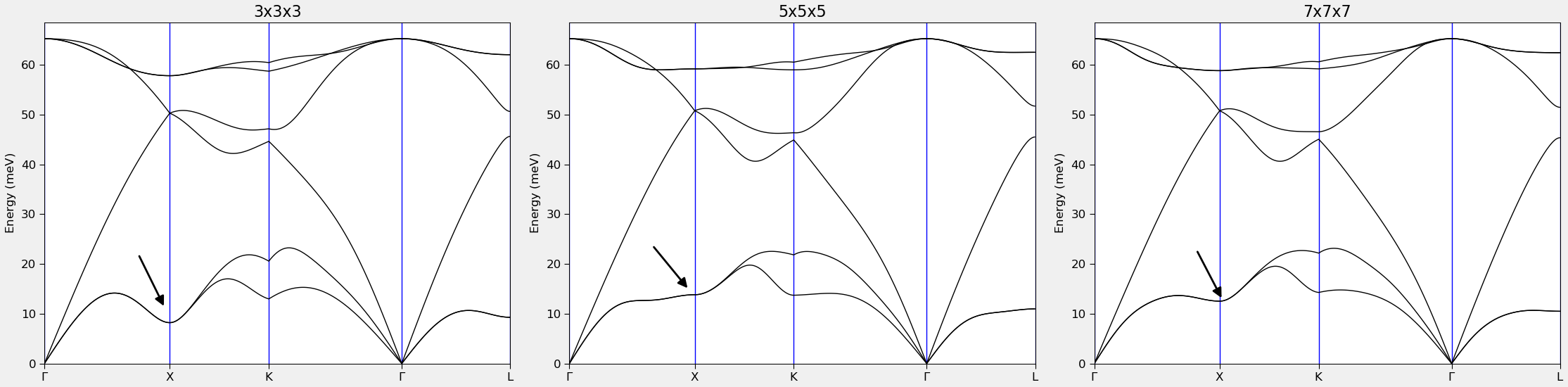
You immediately notice that the 3x3x3 repetition is too small to give even qualitatively good results, while the intermediate size system is already a pretty decent approximation. However, you can also notice that a small difference exists between the acoustic modes near the X-point for the 5x5x5 and the 7x7x7 systems.
The dynamical matrix is now stored together with the BulkConfiguration.
This means you can read the dynamical matrix and perform another PhononBandstructure calculation (on a different Brillouin path
for example) or a PhononDensityOfStates calculation in just a few seconds.
Speeding up the calculation with ForceFields¶
QuantumATK offers a large set of classical potentials in the ForceFieldCalculator. These potentials are well suited to study vibrational properties of materials, such as the phonon bandstructure of silicon calculated in this tutorial.
Note
Classical potentials are available only for a limited amount of systems. As your system becomes more complex including e.g. interfaces, defects or many elements you will often find that no relevant classical potentials exist. In this case QuantumATK offers the ability to train your own machine learned potential using Moment Tensor Potentials. Please get in touch if you would like to try out this functionality and do not have access already.
Send the silicon bulk configuration to the Workflow Builder. Add a ForceFieldCalculator. Now a stress optimization and phonon bandstructure calculation can be set up as explained above.
In ForceFieldCalculator select the most appropriate potential available for silicon, such as the Tersoff or the Stillinger and Weber potentials.
Each potential is provided with a literature reference, which you should check to determine if the potential is well suited for your system and for the property you are interested in.
Set up the OptimizeGeometry block and the PhononBandstructure analysis object exactly as for the LCAOCalculator case and run the calculation. The calculation will take just a few seconds on a normal desktop machine.
The phonon bandstructure of silicon calculated with the Tersoff_si_2005 potential [1] is reported in the figure below.
References