Pseudopotentials and basis sets available in QuantumATK¶
The accuracy of the calculations with the LCAO model in QuantumATK depends on the pseudopotential and basis sets used for the calculations. In recent years we have put a large effort into providing a robust set which can provide good accuracy at reasonably computational resources. Thus, there is an evolution in quality of the pseudopotentials we provide, with the best sets being the SG15 pseudopotentials available from the ATK-2016 release and PseudoDojo pseudopotentials available from the O-2018.06 release. The theoretical background of the basis sets and pseudopotentials are described in the QuantumATK Manual, and the purpose of this note is to guide the user towards the best setting.
Pseudopotentials¶
The pseudopotentials available for the QuantumATK software are listed in the below table. We see that it shows an evolution with quality of the pseudopotentials for each release. However, not all exchange correlation functionals are available for each type of pseudopotential. For GGA and SOGGA we recommend to use the PseudoDojo pseudopotential. For LDA we recommend the FHI pseudopotential. For SOLDA we recommend the OMX, it can also give higher accuracy for LDA, however, the required mesh cutoff needs to be tested carefully.
Name |
Notes |
|---|---|
FHI |
Trouiller–Martins type. |
HGH |
Hartwigsen–Goedecker–Hutter type. |
OMX |
Fully relativistic. OMX webpage. |
SG15 |
ONCV type, scalar-relativistic (SG15) and fully relativistic (SG15-SO). SG15 webpage. |
PseudoDojo |
ONCV type, scalar-relativistic (PseudoDojo) and fully relativistic (PseudoDojo-SO). PseudoDojo webpage. |
GPAW |
PAW potentials. GPAW webpage. |
JTH |
PAW potentials. JTH webpage. |
Suggested |
A mixture of GPAW and JTH, chosen to give optimal results for each element. |
Through the use of the keyword NormConservingPseudoPotential, it is also possible to specify a pseudopotential from a user-specified file. Not all pseudopotentials are available for all QuantumATK DFT calculators and exchange-correlation functional types. Please see the following table for details on each of the pseudopotential types:
Name |
Introduced |
Basis types |
XC-types |
Cutoff [Ha] |
Accuracy |
Efficiency |
|---|---|---|---|---|---|---|
FHI |
ATK-2008 |
LCAO, PW |
LDA, GGA, MGGA, HGGA |
30-100 |
Low |
High |
HGH |
ATK-2011 |
LCAO, PW |
LDA, GGA, MGGA, HGGA |
75-500 |
Medium |
Low |
OMX |
ATK-2015 |
LCAO |
LDA, GGA, MGGA |
75-500 |
High |
Low |
OMX-SO |
ATK-2015 |
LCAO |
SOLDA, SOGGA, SOMGGA |
75-500 |
High |
Low |
SG15 |
ATK-2016 |
LCAO, PW |
GGA, HGGA |
30-220 |
High |
Medium |
SG15-SO |
ATK-2016 |
LCAO, PW |
GGA, SOGGA, HSOGGA |
30-220 |
High |
Medium |
PseudoDojo |
O-2018.06 |
LCAO, PW |
GGA, HGGA |
30-125 |
High |
Medium |
PseudoDojo-SO |
P-2019.03 |
LCAO, PW |
GGA, SOGGA, HSOGGA |
30-125 |
High |
Medium |
PAW-GPAW |
Q-2019.12 |
PW |
LDA, GGA |
N/A |
High |
Medium |
PAW-JTH |
Q-2019.12 |
PW |
LDA, GGA |
N/A |
High |
Medium |
PAW-Suggested |
Q-2019.12 |
PW |
GGA |
N/A |
High |
Medium |
Warning
The higher values for OMX pseudopotentials, about 300 Hartree or more, are especially relevant for pseudopotentials with semi-core states. They often need these very high mesh cutoffs to give accurate forces.
LCAO basis sets¶
QuantumATK mainly uses a numerical LCAO basis sets. The accuracy depends on the number of orbitals and the range of the orbitals. Increasing the number of orbitals and their range decrease the efficiency and increase the memory requirement. For the latest SG15 and PseudoDojo pseudopotentials we provide basis sets which systematically improve the accuracy. For the other pseudopotentials the improvement in accuracy is less systematic.
SG15/PseudoDojo¶
Three different basis sets are available for each element when using the SG15/PseudoDojo pseudopotentials; Medium, High, and Ultra. All three derive from the numerical atom-centered basis sets of the FHI-aims package, but have been significantly modified and optimized with respect to computational speed with the DFT: LCAO calculator.
The Medium basis set is default for the SG15/PseudoDojo pseudopotentials, and should be sufficient for most applications. However, if extreme accuracy is needed, the High and Ultra basis sets add more basis functions at the expense of increased computational load.
OMX¶
The OMX basis sets were developed in Refs. [1] and [2], and are optimized towards maximum computational speed and accuracy with the OMX pseudopotentials. The DFT: LCAO calculator offers three different OMX basis set sizes for most elements; Low, Medium, and High, which include increasingly more pseudo-atomic orbitals in the basis set. More details are available on the website for the OpenMX database (2013).
FHI¶
Four different types of basis functions can be used for the FHI pseudopotentials:
The basis sets available for FHI pseudopotentials are listed below. They are ordered with increasing number of basis orbitals – those with more orbitals are often more accurate, at the expense of increased computational load. The DZP basis set is default.
SingleZeta: One ConfinedOrbital for each occupied valence orbital in the atom.
DoubleZeta: One ConfinedOrbital and one AnalyticalSplit for each occupied valence orbital in the atom.
SingleZetaPolarized: One ConfinedOrbital for each occupied valence orbital in the atom, and one PolarizationOrbital for the first unoccupied shell in the atom.
DoubleZetaPolarized: One ConfinedOrbital and one AnalyticalSplit for each occupied valence orbital in the atom. One PolarizationOrbital for the first unoccupied shell in the atom.
DoubleZetaDoublePolarized: One ConfinedOrbital and one AnalyticalSplit for each occupied valence orbital in the atom. One PolarizationOrbital and one AnalyticalSplit for the first unoccupied shell in the atom.
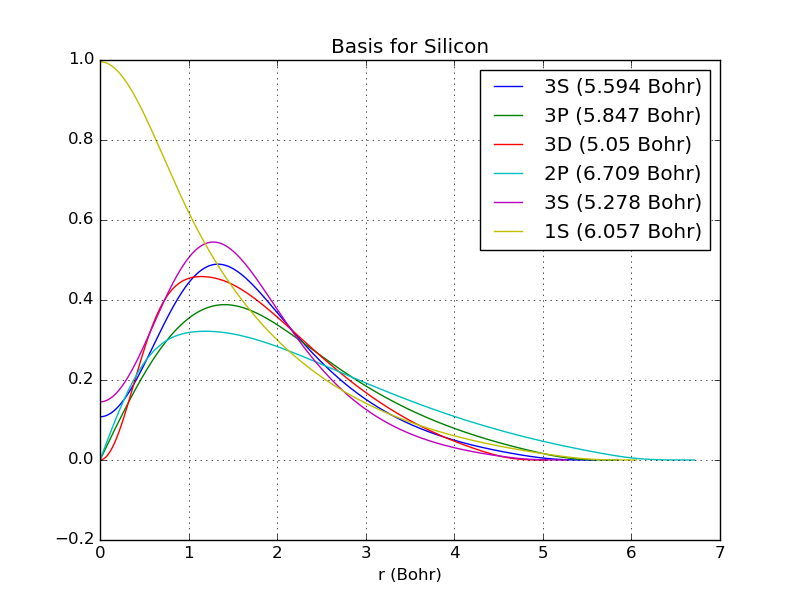
Visualizing the basis functions¶
To see the type of the basis sets it is most easy to plot the basis functions, like this:
Open the scripter
Add an LCAOcalculator block from the Calculators section
Go to the Basis set tab at click the plot widget
 in the line where you define the basis set.
in the line where you define the basis set.

You will then get the following plot.
Accuracy tests for elemental solids¶
To give an overall idea of the accuracy of each pseudopotential and basis sets we have performed so-called \(\Delta\)-tests [3] (see the web-site Comparing Solid State DFT Codes, Basis Sets and Potentials). These tests checks accuracy for the pseudopotential and basis set compared with state of the art all-electron calculations. The tests check the accuracy of the pseudopotential and basis sets in reproducing the equation of state of all the elemental solids in the periodic system using the GGA-PBE exchange-correlation functional.
Pseudo |
Basis |
\(\Delta\) (meV) |
Performance |
|---|---|---|---|
FHI |
SZP |
39.4 |
0.5 |
FHI |
DZP |
18.2 |
1 |
FHI |
DZDP |
19.1 |
2 |
HGH |
Tier4 |
12.8 |
6 |
OMX |
Medium |
8.0 |
3 |
OMX |
High |
2.2 |
10 |
SG15 |
Medium |
3.45 |
2 |
SG15 |
High |
1.88 |
6 |
SG15 |
Ultra |
2.03 |
25 |
SG15 |
PW |
1.32 |
N/A |
PseudoDojo |
Medium |
4.53 |
2 |
PseudoDojo |
High |
1.52 |
6 |
PseudoDojo |
Ultra |
1.40 |
25 |
PseudoDojo |
PW |
1.04 |
N/A |
PAW-GPAW |
PW |
1.44 |
N/A |
PAW-JTH |
PW |
0.86 |
N/A |
PAW-Suggested |
PW |
0.64 |
N/A |
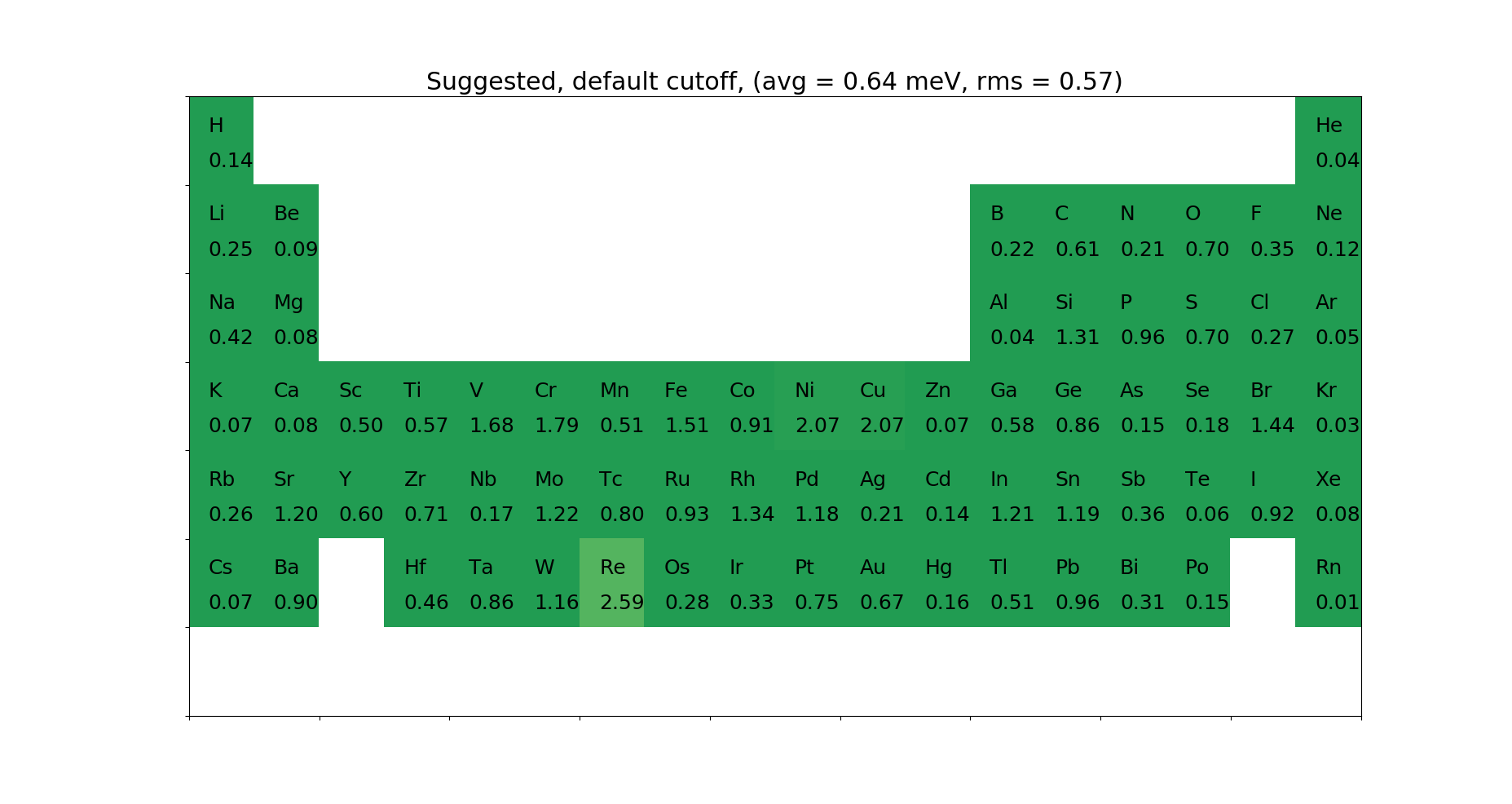
A \(\Delta\) value below 2 meV indicates a state of the art DFT calculation. PAW-Suggested is a combination of the two PAW sets where we have selected the best PAW potential for each element. The performance number given in the Table is an average indication of how much time a calculation of a 64 atom supercell takes, using the different models relative to the FHI-DZP model. Lower numbers are faster. There are large variations among the elements and the performance number should only be used as a rough guide.
Accuracy tests for mixed solids¶
The \(\Delta\)-tests are done for ideal systems, in order to illustrate that these results are transferable to general systems we have performed a number of additional accuracy tests. The first test is for a number Rock Salt (RS) and Perovskite(P) structures provided in Ref. [4]. The reference points are FHI-aims all electron calculations. We see the deviations for the \(a\) (lattice constant), \(B\) (Bulk modulus) and \(E_f\) (formation energy) compared to the Ref. [4] in the below Table.
Pseudo |
Basis |
\(a\) (%) |
\(B\) (%) |
\(E_f\) (%) |
Source |
|---|---|---|---|---|---|
Ultra-Soft |
PW |
0.13 |
5.0 |
N/A |
|
PAW |
PW |
0.15 |
4.5 |
N/A |
|
PseudoDojo |
Ultra |
0.15 |
1.90 |
1.83 |
QuantumATK |
PseudoDojo |
High |
0.18 |
2.12 |
2.79 |
QuantumATK |
PseudoDojo |
Medium |
0.5 |
5.32 |
15.59 |
QuantumATK |
PseudoDojo |
PW (40 Ha) |
0.09 |
1.86 |
0.85 |
QuantumATK |
SG15 |
High |
0.3 |
8.6 |
4.6 |
QuantumATK |
SG15 |
Medium |
0.6 |
13.0 |
12.5 |
QuantumATK |
FHI |
DZP |
3.0 |
23.2 |
15.5 |
QuantumATK |
Pseudo |
Basis |
\(a\) (%) |
\(B\) (%) |
\(E_f\) (%) |
Source |
|---|---|---|---|---|---|
Ultra-Soft |
PW |
0.08 |
5.5 |
N/A |
|
PAW |
PW |
0.13 |
6.1 |
N/A |
|
PseudoDojo |
Ultra |
0.13 |
1.87 |
0.91 |
QuantumATK |
PseudoDojo |
High |
0.21 |
3.04 |
1.18 |
QuantumATK |
PseudoDojo |
Medium |
0.35 |
3.68 |
2.73 |
QuantumATK |
PseudoDojo |
PW (40 Ha) |
0.06 |
0.66 |
0.23 |
QuantumATK |
SG15 |
High |
0.3 |
5.7 |
1.4 |
QuantumATK |
SG15 |
Medium |
0.4 |
6.4 |
2.6 |
QuantumATK |
FHI |
DZP |
3.5 |
18.3 |
12.8 |
QuantumATK |
Notes for each pseudopotential type¶
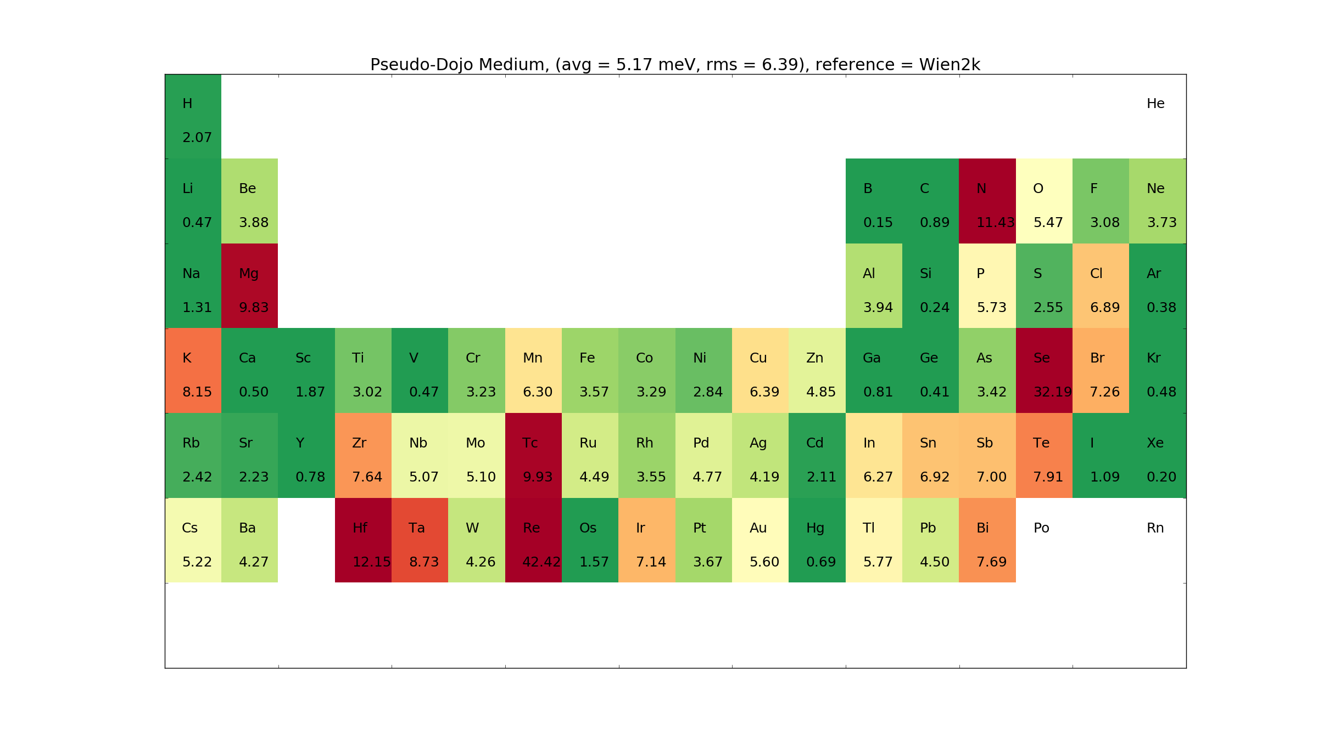
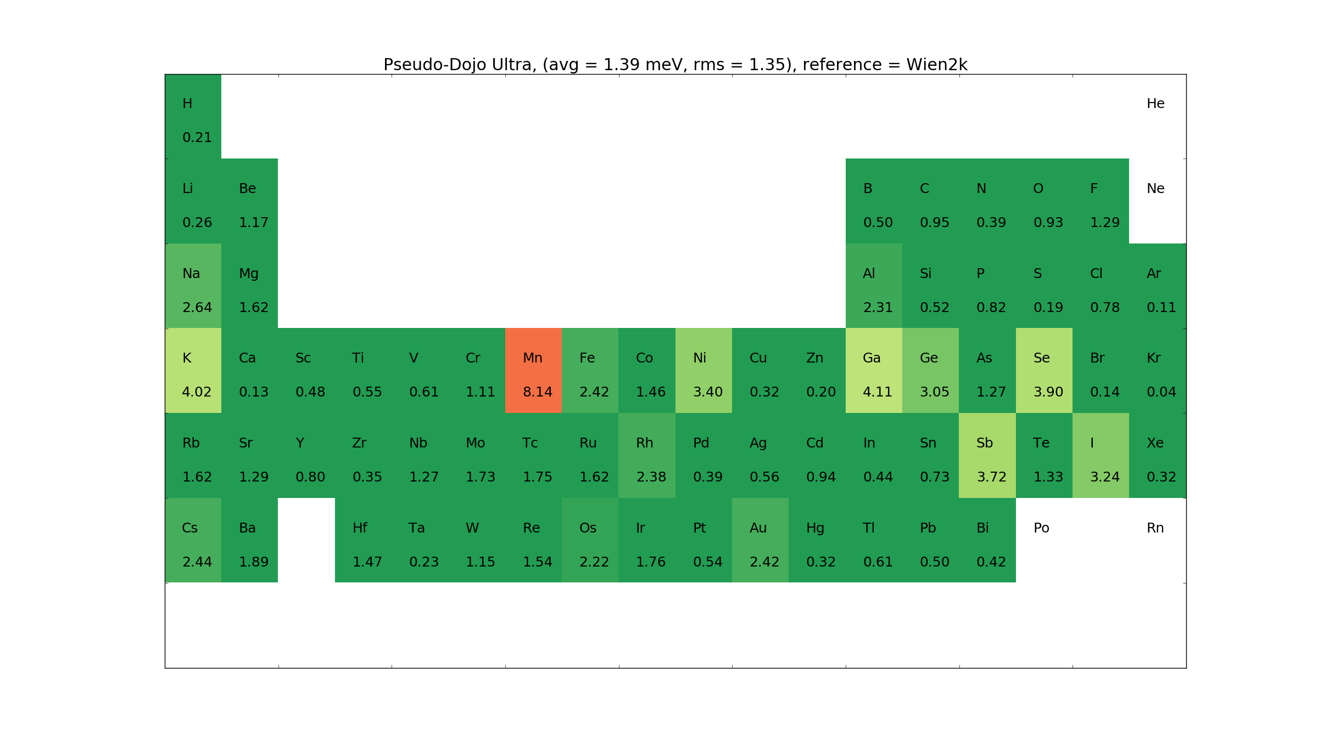
PseudoDojo Pseudopotentials and basis sets¶
The PseudoDojo are state of the art norm-conserving pseudopotentials including multiple projectors, semi-core states and non-linear core correction [5]. They are only provided for the GGA-PBE functional, and comes in both a scalar relativistic and a fully relativistic version. The latter is used for calculations including spin-orbit. The pseudopotentials are smooth and all elements converge with a mesh cutoff below 125 Ha.
A large effort has been put into providing high accuracy basis sets. Three sets are provided: Ultra, High and Medium. The basis sets have been optimized to describe bulk systems, dimers and trimer systems.
Below are given the \(\Delta\)-tests for the different elements.


SG15 Pseudopotentials and basis sets¶
The SG15 are state of the art norm-conserving pseudopotentials including multiple projectors, semi-core states and non-linear core correction [6][7]. They are only provided for the GGA-PBE functional, and comes in a scalar relativistic and a fully relativistic version. The latter is used for calculations including spin-orbit. The pseudopotentials are smooth and all elements converge with a mesh cutoff below 220 Ha.
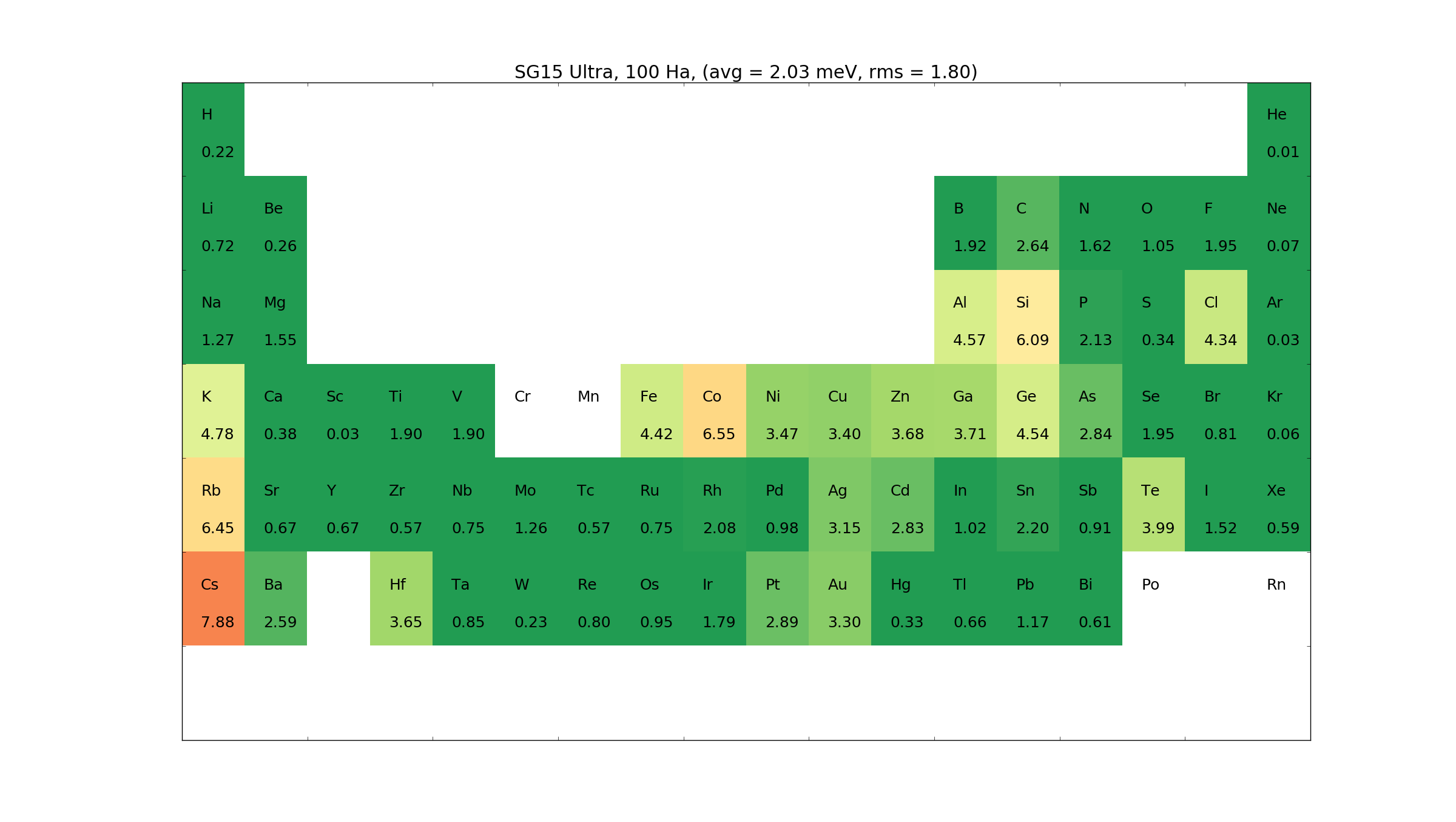
A large effort has been put into providing high accuracy basis sets. Three sets are provided: Ultra, High and Medium. The basis sets have been optimized to describe bulk systems, dimers and trimer systems.
Below are given the \(\Delta\)-tests for the different elements.


PAW data sets¶
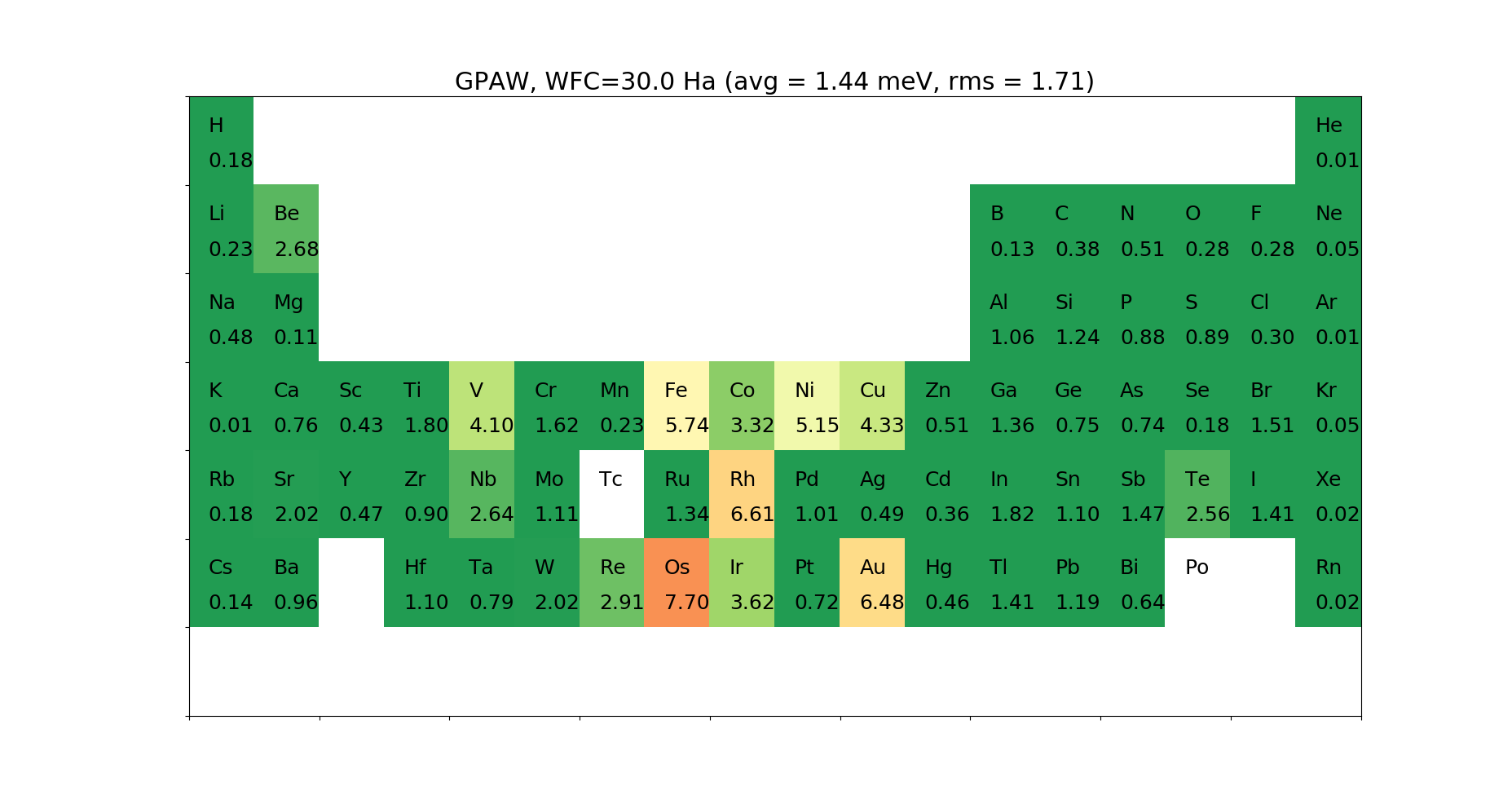
For the Projector Augmented Wave (PAW) method, we need data describing the system inside the augmentation sphere (partial waves, projectors, core densities, …). This is gathered in a PAW data set file. We support data set files in the .xml format, as specified on the ESL website. We ship two different data sets, the GPAW and JTH [8] data sets, for which we found default wave function cutoffs that are as low as possible without losing accuracy. We made a combined PAW-Suggested data set for GGA, that gives the best results.
Below are given the \(\Delta\)-tests for the different elements.

FHI pseudopotentials and basis sets¶
The FHI pseudopotentials are the oldest pseudopotentials in QuantumATK. These pseudopotentials are generated with the Fritz-Haber Institute (FHI) pseudopotential code. They are numerical norm-conserving pseudopotentials with a single projector for each angular momentum and without semicore states. For a number of elements the exclusion of semi-core states gives a low accuracy.
The basis sets provided with the FHI pseudopotentials use generic parameters, which are not optimized for each element and generally not of high accuracy. However, the basis sets and pseudopotentials are rather efficient and for some elements can give satisfactory accuracy. We only recommend the SZP and DZP basis sets. Below are given \(\Delta\) values for these settings and the table can be used to estimate the accuracy of the model for various elements.


OMX Pseudopotentials and basis sets¶
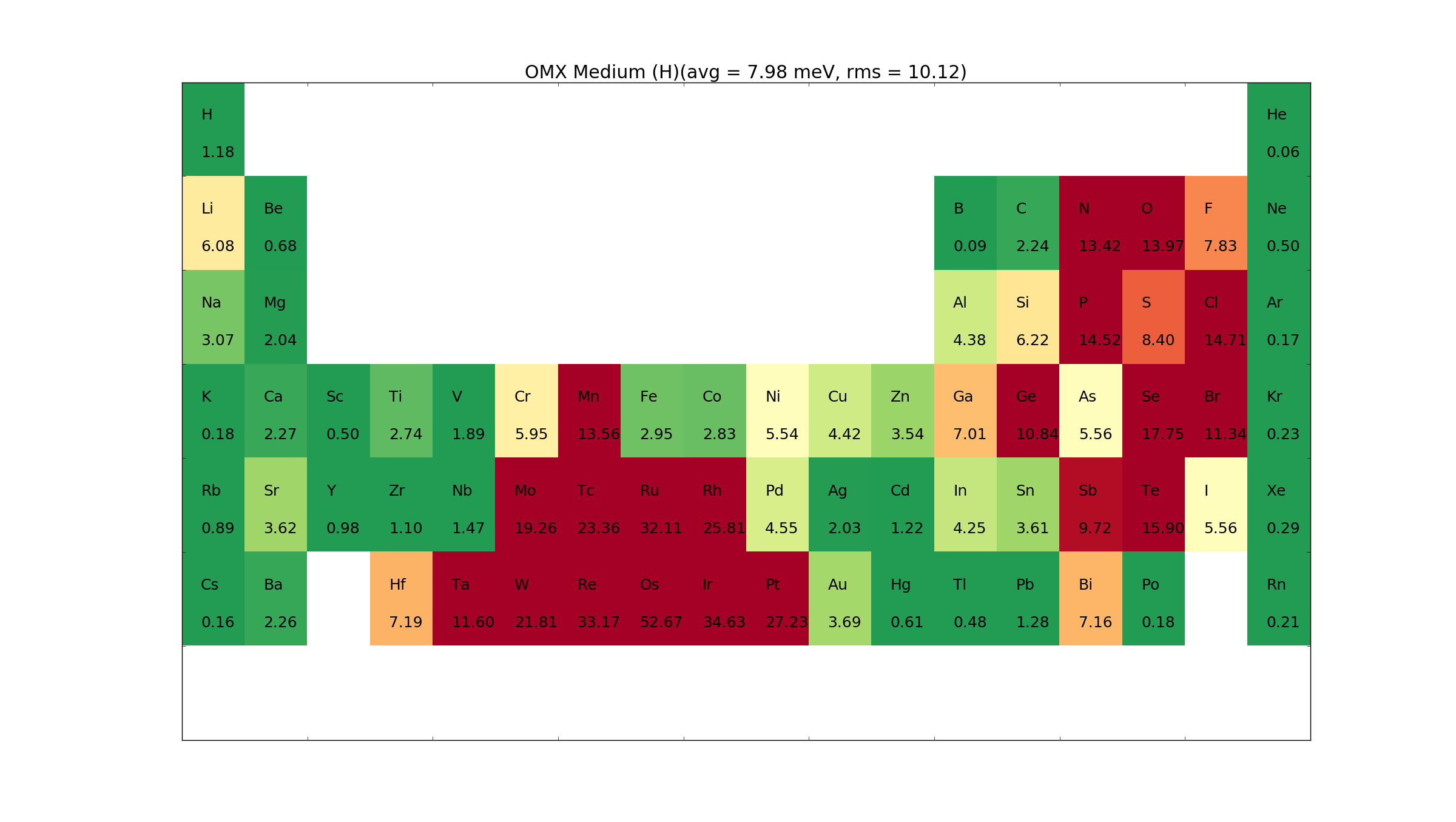
The OMX pseudopotentials are from the OpenMX packages. They are fully relativistic, multiple projectors and with semi-core states. Thus, these are generally high accuracy pseudopotentials which can be used for both LDA, GGA and spin-orbit calculations. The drawback of the pseudopotentials is that they for some elements require very high mesh cutoffs.
The basis sets provided are from the original openMX package. This means that they are not calculated on the fly, and therefore only accurate for the exchange-correlation potential for which they were calculated. Thus, if other exchange-correlation functionals than LDA-PZ or GGA-PBE are used, the accuracy will be lower. For our other pseudopotentials the basis sets are generated on the fly with the selected exchange-correlation potential, thus, even if the pseudopotential is not generated for the exchange-correlation functional the basis set will conform to the exchange-correlation functional.
For the OMX pseudopotentials, we have defined two basis set types, Medium and High. It is also possible for the user to define custom basis sets through the atomic_species keyword, see OpenMXBasisSet.
The basis sets was pre-calculated using GGA-PBE or LDA-PZ and included together with the pseudopotential. Thus, if other exchange-correlation functionals than LDA-PZ or GGA-PBE are used, the accuracy will be low.
For the other pseudo potentials the basis sets are calculated on the fly, using the selected exchange-correlation potential. i.e. only core electrons are treated with the GGA-PBE functional, while valence electrons are treated with the selected exchange-correlation functional.
Below we provide the \(\Delta\) values for the Medium and High basis sets. For the High basis set we also provide the \(\Delta\) value when a 100 Ha mesh cutoff is used. This, gives an indication for which elements the default mesh cutoff needs to be increased.


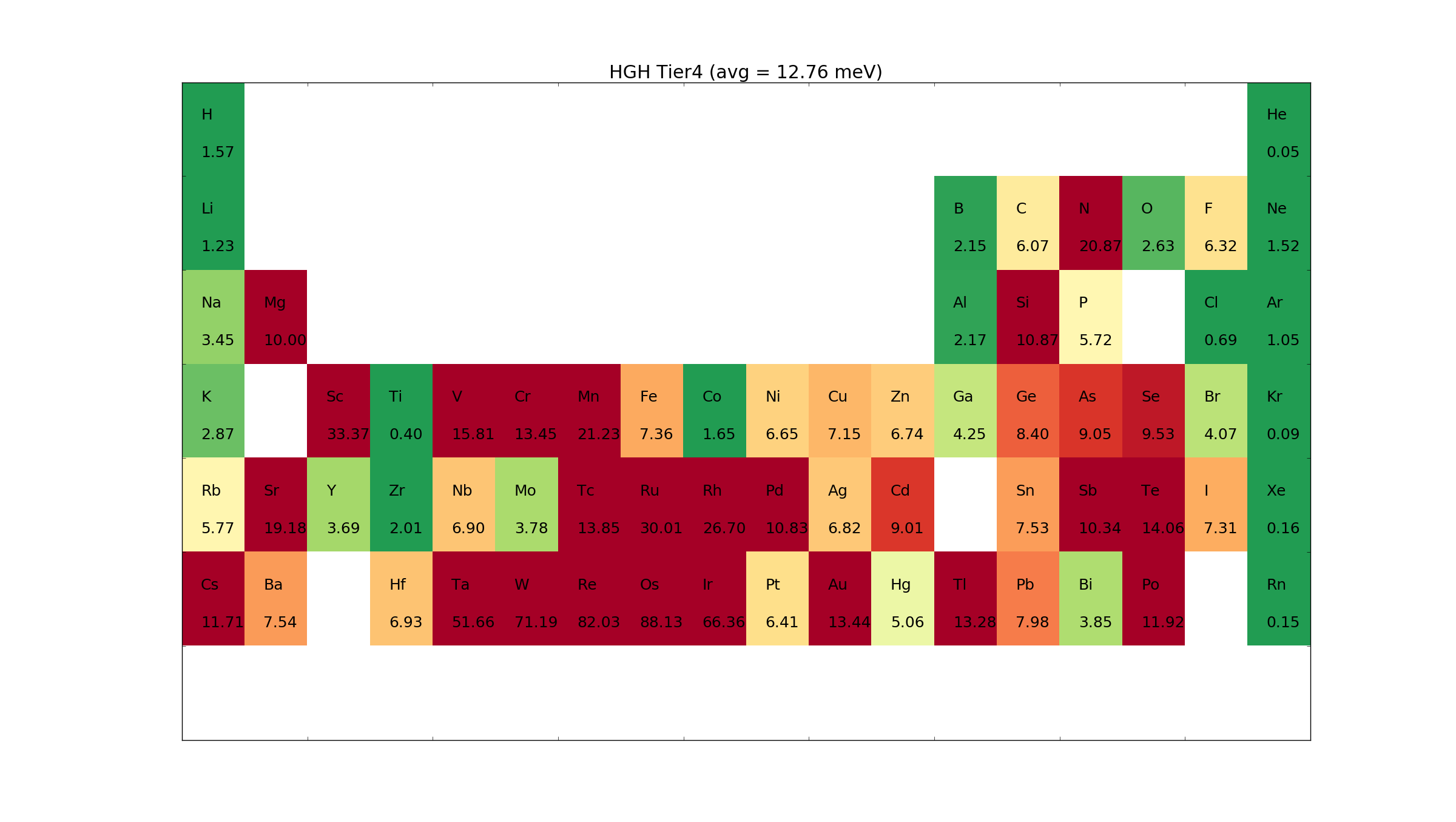
HGH Pseudopotentials and basis sets¶
The Hartwigsen–Goedecker–Hutter (HGH) type pseudopotentials are also norm-conserving pseudopotentials, however, include multiple projectors and semi-core states. The pseudopotentials use analytical functions which are slightly lower accuracy than numerical pseudopotentials. These pseudopotentials require high values for the mesh cutoff for some elements.
For each pseudopotential we provide a hierarchy of basis sets. The basis sets were optimized to describe the total energy of dimers with different bondlengths. This was an early version of our basis set optimization tool and not all elements are well described.
Generally the pseudopotentials and basis sets have better accuracy than the FHI pseudopotentials but can be computationally heavy and require high mesh cutoffs. The sets are only provided for backwards compatibility and are no longer recommended.