Electronic Properties of Phase Change Material Ge₂Sb₂Te₅

Version: T-2022.03

In this tutorial, we will investigate electronic properties of Ge₂Sb₂Te₅, a phase change material used in non-volatile memory technology, using Density Functional Theory (DFT) calculations. Please follow the tutorial Band Structure of a SiC Crystal to familiarize yourself with the use of scripter to set up calculations. Only the final scripts will be provided in this tutorial.

Geometry

For this tutorial, let us first download the unitcell configuration of Ge₂Sb₂Te₅, in a trigonal crystal system with hexagonal lattice symmetry, from the materials project database (mp-1224375) using the Database Tool available in the NanoLab. For reference, the geometry can also be downloaded from here GST-geometry.py.

Bandgap Calculation

As the first property, let us compute the bandgap of Ge₂Sb₂Te₅ and compare to literature data. To do that, the unit cell geometry will be optimized with space group constraint for minimum energy first and then its BandStructure will be computed. Additionally, we will compare the default GGA (PBE XC functional) results to more accurate HSE06 calculations using the PseudoDojo LCAO basis sets. To be exact, 4 different calculation settings will be used as follows:

• PBE functional based geometry relaxation and BandStructure calculation(PBE.py)

• HSE06 hybrid functional based geometry relaxation and BandStructure calculation(HSE.py)

• HSE06 hybrid functional with ADMM basis set for both geometry relaxation and BandStructure calculation(HSE-ADMM.py)

• PBE functional based geometry relaxation followed by HSE06 hybrid XC functional based BandStructure calculation(PBE-HSE.py)

The bandgap can be quickly viewed from the BandStructure object preview window or from the BandStructure Analyzer object. The corresponding results of the above calculations (using 40 MPI processes in 1 node) are given in the below image.

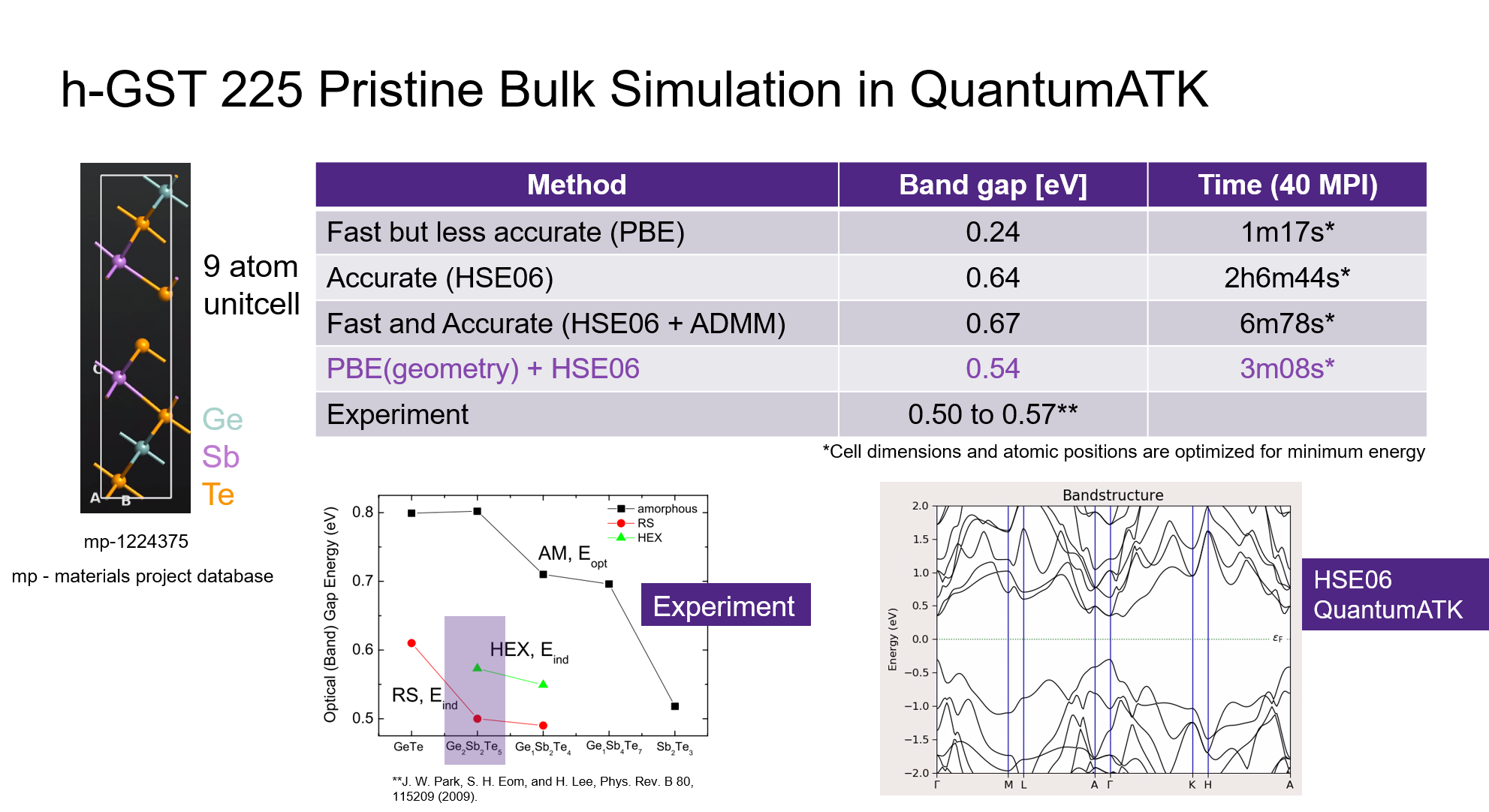
Experimental bandgap of hexagonal Ge₂Sb₂Te₅ is known to be between 0.50 and 0.57 eV [1]. PBE only calculation is the fastest but the bandgap is underestimated to 0.24 eV only. Standard HSE06 calculation took over 2 hours and gave a bandgap of 0.64 eV. Inclusion of ADMM basis sets accelerated the HSE06 calculation to completion within 7 minutes and produced a similar bandgap. However, HSE06 based bandstructure calculation on PBE optimized geometry gave a better bandgap value of 0.54 eV while taking only about 3 minutes.

Lattice Parameters

Lattice parameters of the Ge₂Sb₂Te₅ unitcell after geometry optimization using the PBE and HSE06 functionals are given in the below image.

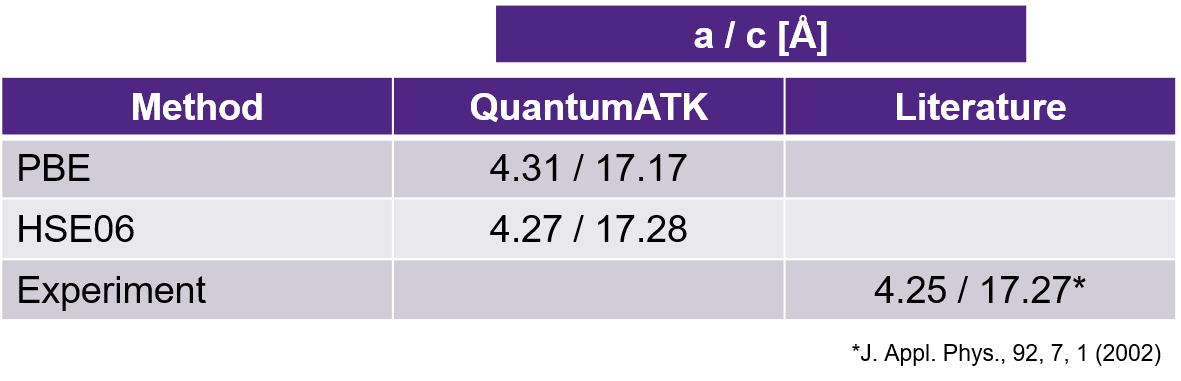
Both PBE and HSE06 optimized geometries have lattice parameters within 0.1 Å of the experimental values [2].

Cohesive Energies

Cohesive energies of the Ge₂Sb₂Te₅ is computed using PBE and HSE06 methods using E_bulk - (2*E_Ge + 2*E_Sb + 5*E_Te) and the results are shown below. Here, E_bulk is the total energy of bulk system and E_Ge, E_Sb and E_Te are atomic reference energies of Ge, Sb and Te, respectively.

In the above results, two different sets of reference energy values are used for the elemental contributions. First set of cohesive energies (top of the picture) are computed using total energies of isolated Ge, Sb and Te atoms as reference and match well with literature [3]. The following scripts are used for the above reference calculations (Ge (HSE, PBE), Sb (HSE, PBE), Te (HSE, PBE)). For the second set, total energies per atom in homogeneous bulk systems are used. The corresponding scripts are attached here (Ge, Sb, Te). Reference cohesive energy is calculated using the data from materials project database using the following IDs (GST:mp-1224375, Ge:mp-32, Sb:mp-104, Te:mp-19). From the above image, we find that our calculations agree reasonably with the published calculated reference values within 4 meV/atom for isolated atom reference and within 20 meV/atom for bulk reference. Note that the literature reference uses a different basis set and calculator settings.

Neutral Vacancy Formation Energies

In this section, we compute the formation energies of neutral vacancies within a unitcell of Ge₂Sb₂Te₅ using PBE XC functional and compare to literature results [4]. The formation energy of a single neutral vacancy is obtained as E_{pristine GST} - (E_{GST with vacancy} + E_{bulk reference}), where E_{bulk reference} is the energy of the removed atom in its bulk state.

We perform three vacancy calculations by removing either one Ge, one Sb or one Te atom from the unitcell geometry as highlighted in the above image and replacing them with a ghost atom. A ghost atom is used to include the basis functions for that removed atom in the calculation. The corresponding scripts are given here (Ge-vacancy, Sb-vacancy, Te-vacancy). As can be seen from the above image, the formation energy of Ge vacancy is the lowest followed by Te and Sb. This ordering is similar to the literature results with some discrepancies in the absolute values. This could be attributed to the different lattice parameters and basis sets (reference: plane wave basis and PAW, QuantumATK: LCAO and PseudoDojo medium) used in the literature reference and in our calculations.

Total DOS With and Without Ge Vacancy

In this section we compare the total density of states from the GST (5x1x1) supercell with and without a Ge vacancy and compare the results to literature [4]. The scripts used for this calculation can be downloaded from these links (Pristine, VGe).

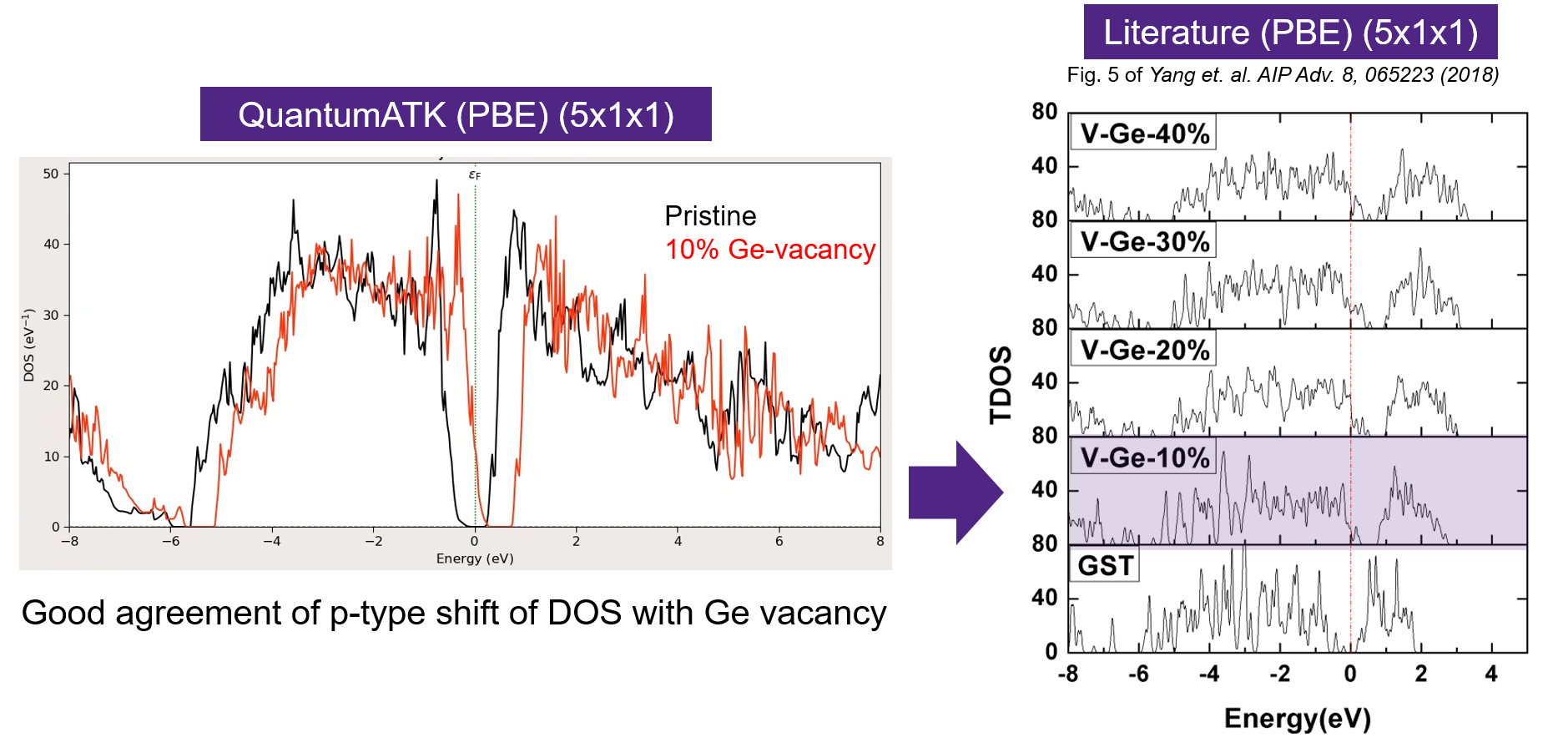
The above plot shows the DOS comparison and a clear p-type shift is observed on including 10% Ge vacancy. This observation is in good qualitative agreement with the reference.

[1]

Jun-Woo Park, Seung Hwan Eom, Hosun Lee, Juarez LF Da Silva, Youn-Seon Kang, Tae-Yon Lee, and Yoon Ho Khang. Optical properties of pseudobinary GeTe, Ge2Sb2Te5, GeSb2Te4, GeSb4Te7, and Sb2Te3 from ellipsometry and density functional theory. Physical Review B, 80(11):115209, 2009.

[2]

BJ Kooi and J Th M De Hosson. Electron diffraction and high-resolution transmission electron microscopy of the high temperature crystal structures of GexSb2Te3+x (x= 1,2,3) phase change material. Journal of applied physics, 92(7):3584–3590, 2002.

[3]

Baisheng Sa, Jian Zhou, Zhitang Song, Zhimei Sun, and Rajeev Ahuja. Pressure-induced topological insulating behavior in the ternary chalcogenide Ge2Sb2Te5. Physical Review B, 84(8):085130, 2011.

[4] (1,2)

Fei Yang, Tian Chen, Minglei Wang, Beibei Yan, Luxu Wan, Daoming Ke, and Yuehua Dai. First-principles study of the properties for crystal Ge2Sb2Te5 with Ge vacancy. AIP Advances, 8(6):065223, 2018.