FragmentGenerator¶
- class FragmentGenerator(vacuum_length=None, buffer_length=None, fractional_coordinates_cuts=None, number_of_minimal_fragments=None, fragment_lengths=None, fuzz_factor=None, passivation_parameters=None)¶
Class for generating fragments of a bulk configuration.
- Parameters:
vacuum_length (float of PhysicalQuantity type length) – The thickness at each boundary that should be covered with vacuum. Default:
5.0 * Angstrom.buffer_length (float of PhysicalQuantity type length) – The thickness at each boundary that should be filled with existing adjacent atoms from the adjacent fragments. Default:
0.0 * Angstrom.fractional_coordinates_cuts (list of size 3 of floats in range (0, 1) or None) – The cuts in fractional coordinates along the primitive vectors of the cell. NOTE: A None element means that the given dimension should not be fragmented. This option is mutually exclusive to
number_of_minimal_fragmentsandfragment_lengths.number_of_minimal_fragments (tuple (size 3) of either None or positive int) – The number of fragments in each directions of the cell. NOTE: A None element means that the given dimension should not be fragmented. This option is mutually exclusive to
fractional_coordinates_cutsandfragment_lengths.fragment_lengths (float of PhysicalQuantity type length | list (size 3) of None or floats of PhysicalQuantity type length) – The length of each fragment dimension. NOTE: A None element means that the given dimension should not be fragmented. If a single PhysicalQuantity is provided, this will be used in all directions. This option is mutually exclusive to
number_of_minimal_fragmentsandfractional_coordinates_cuts.fuzz_factor (float) – The factor by which the covalent radii are multiplied to determine the cutoff distance for a bond. Default:
1.1passivation_parameters (Flag All or NoPassivation of
NLFlagor a list of tuples (size 2) with an element and a flag or basis set.) – Parameter(s) to specify passivation. Default:All
- bufferLength()¶
- Returns:
The buffer_length.
- Return type:
PhysicalQuantity of type length
- fractionalCoordinatesCuts()¶
- Returns:
The fractional_coordinates_cuts.
- Return type:
list of tuples of floats in range (0, 1) or None
- fragmentLengths()¶
- Returns:
The fragment_lengths.
- Return type:
list (size 3) of None or floats of PhysicalQuantity type length
- fragmentationDimensionality()¶
- Returns:
Which of the 3 spacial directions to create fragments in.
- Return type:
A tuple (size 3) of bool.
- fuzzFactor()¶
- Returns:
The factor by which the covalent radii are multiplied to determine the cutoff distance for a bond.
- Return type:
float
- minimalFragmentLength()¶
- Returns:
The minimal fragment length.
- Return type:
PhysicalQuantity of type length
- nlinfo()¶
- Returns:
Structured information about the FragmentGenerator.
- Return type:
dict
- numberOfMinimalFragments()¶
- Returns:
The number_of_minimal_fragments.
- Return type:
tuple (size 3) of either None or positive int or None
- passivationParameters()¶
- Returns:
Parameter(s) to specify passivation.
- Return type:
Flag All or NoPassivation of
NLFlagor a list of tuples (size 2) with an element and a flag or basis set.
- uniqueString()¶
Return a unique string representing the state of the object.
- vacuumLength()¶
- Returns:
The vacuum_length.
- Return type:
PhysicalQuantity of type length
Usage Examples¶
The FragmentGenerator must be defined in connection with the FragmentCalculator to specify the fragmentation of a larger system configuration. Both classes are fully dependent on each other. The FragmentGenerator provides three mutually exclusive options for fragmentation:
fractional_cutsnumber_of_minimal_fragmentsfragment_lengths
Note that these fragmentation approaches determine the dimensions of the minimal fragments (also termed single fragments).
The fractional_cuts option instructs some cuts along the primitive vectors of the unit cell. This is illustrated in Fig. 156 as the fractional divisions along the C primitive vector.
# Cut the C primitive vector into 3 equal lengths.
fractional_cuts = [None, None, [1/3, 2/3]]
Note
The None inputs in the fractional_cuts vector indicate that no fragmentation should be performed along the A- and B directions.
For the C-direction, the fractional cuts at 0 and 1 are implicit and should not be specified.
The number_of_minimal_fragments option specifies a certain number of divisions along the primitive vectors of the unit cell as illustrated in Fig. 156.
# Divide the full system into 3 single fragments along the C primitive vector.
number_of_minimal_fragments = [1, 1, 3]
Here, the numbers 1 again implies that no fragmentation will be performed along the A- and B directions.
The fragment_lengths option simply divides the primitive vectors in lengths of physical units accordingly,
# For the purpose of this example, say L = 5 Angstrom.
L = 5 * Angstrom
fragment_lengths = [None, None, L]
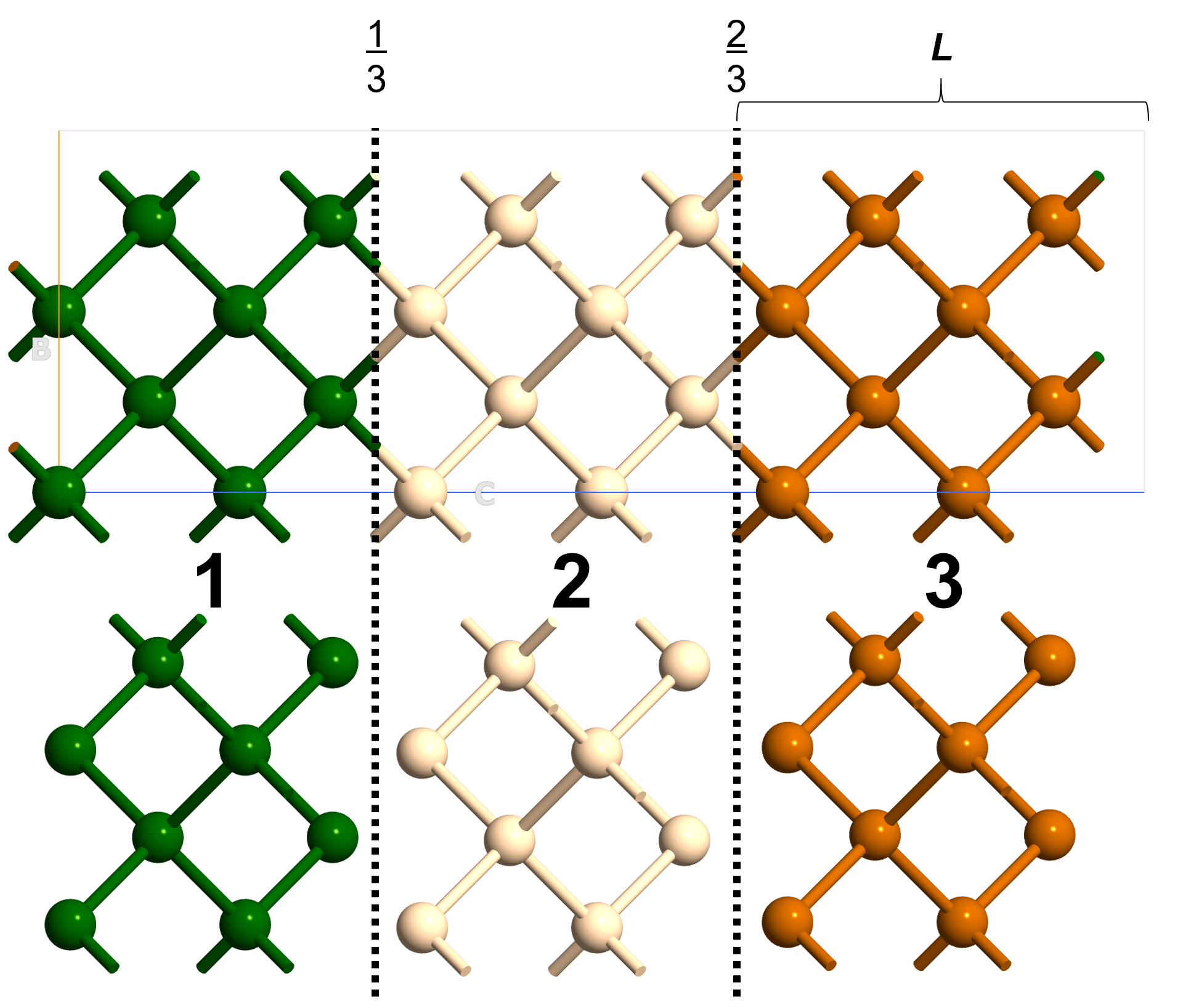
Fig. 156 Fragmentation methods when using FragmentGenerator.¶
After choosing a fragmentation method it can be given as an argument for the FragmentGenerator. It is only possible to use one method.
# Create the fragment generator with the fragmentation method.
fragment_generator = FragmentGenerator(
fragment_lengths=fragment_lengths,
)
Each fragment has its own configuration where the actual fragment atoms are embedded in vacuum. A buffer region may also be included containing atoms from neighboring fragments. The vacuum and buffer regions are specified as input arguments of the FragmentGenerator and only added in the given directions where fragmentation occurs.
# Define fragmentation method.
number_of_minimal_fragments = [1, 1, 3]
# Define vacuum and buffer lengths.
vacuum_length = 6.0 * Angstrom
buffer_length = 3.0 * Angstrom
# Create the fragment generator with the vacuum and buffer lengths and fragmentation method.
fragment_generator = FragmentGenerator(
number_of_minimal_fragments=number_of_minimal_fragments,
vacuum_length=vacuum_length,
buffer_length=buffer_length,
)
Upon fragmentation multiple bonds might be cut between surfaces of fragments. In order to avoid occurrence of metallic surface states, passivation might be required. In some cases one might want to passivate certain elements of fragment configurations or passivate with a particular fractional hydrogen basis set. Therefore, FragmentGenerator can take an input passivation_parameters which applies for all fragment surfaces. Three options are available.
Allflag indicating passivation of all elements.NoPassivationflag indicating no passivation of any elementsA list of elements with respective passivation type in form of either a hydrogen basis set or a flag as in the two points above
# Define fragmentation method.
number_of_minimal_fragments = [1, 1, 3]
# Define passivation parameters. Say that we have a GaAs configuration and we
# want to passivate Ga with 1.25 fractional pseudo hydrogens and As with
# 0.75 fractional pseudo hydrogens.
passivation_parameters = [
(Gallium, FractionalGGABasis.fractional_1_25_HydrogenBasis),
(Arsenic, FractionalGGABasis.fractional_0_75_HydrogenBasis),
]
# Create fragment generator with passivation.
fragment_generator = FragmentGenerator(
number_of_minimal_fragments=number_of_minimal_fragments,
passivation_parameters=passivation_parameters,
)
In all cases, the passivating Hydrogen atoms are positioned in the center of the bond cut by the surface. The definition of when two atoms form a bond is determined by a fuzz_factor. This is equivalent to the fuzz_factor used in the Viewer and Builder for visualizing bonds (this can be modified under Graphics Properties). The default value is 1.1, but in some cases this might need to be increased to e.g. 1.15 in order to include all relevant bonds:
# Define fragmentation method.
number_of_minimal_fragments = [1, 1, 3]
# Create fragment generator with passivation.
fragment_generator = FragmentGenerator(
number_of_minimal_fragments=number_of_minimal_fragments,
fuzz_factor=1.15,
)
1D, 2D, and 3D fragmentation¶
The FragmentGenerator and FragmentCalculator can be used to divide the initial configuration into 1D, 2D or 3D fragments depending on the input to FragmentGenerator as illustrated below:
# 1D fragmentation: Divide the configuration into 5 single fragments.
# Total number of fragment = 10.
fragment_generator = FragmentGenerator(
number_of_minimal_fragments=[None, None, 5],
)
# 2D fragmentation: Divide the configuration into 5x5 = 25 single fragments.
# Total number of fragment = 100.
fragment_generator = FragmentGenerator(
number_of_minimal_fragments=[None, 5, 5],
)
# 3D fragmentation: Divide the configuration into 5x5x5 = 125 single fragments.
# Total number of fragment = 1000.
fragment_generator = FragmentGenerator(
number_of_minimal_fragments=[5, 5, 5],
)
For 1D fragmentation, the fragments generated will either be single fragments, denoted (1,1,1) or double fragments, denoted (1,1,2) for fragmentation along the C-direction.
For 2D fragmentation along B and C directions, the fragments are (1,1,1), (1,2,1), (1,1,2), and (1,2,2). For each single fragment there will be 4 fragments in total. Dividing the configuration into 5x5 single fragments thus results in 100 fragments in total.
For 3D fragmentation the fragments are (1,1,1), (2,1,1), (1,2,1), (1,1,2), (2,2,1), (2,1,2), (1,2,2), (2,2,2) i.e. 8 fragments in total for each single fragment. A 5x5x5 fragmentation thus leads to 1000 fragments in total.
The large number of fragments when performing 3D fragmentation implies that the fragment calculation can be efficiently parallelized over many CPUs, although full parallelization will lead to significant load imbalance.
