NPTBernettiBussi

class NPTBernettiBussi(initial_velocity=None, time_step=None, reservoir_temperature=None, thermostat_timescale=None, reservoir_pressure=None, barostat_timescale=None, compressibility=None, coupling_mask=None, heating_rate=None, compression_rate=None, random_seed=None)

NPT integrator class which implements the stochastic velocity rescaling (Bussi-Donadio-Parrinello) thermostat in combination with the stochastic cell rescaling (Bernetti-Bussi) barostat. It correctly samples the isobaric-isothermic ensemble.

Parameters:

• initial_velocity (ConfigurationVelocities | ZeroVelocities | MaxwellBoltzmannDistribution) – A class that implements a distribution of initial velocities for the particles in the MD simulation.
  Default: MaxwellBoltzmannDistribution

• time_step (PhysicalQuantity of type time) – The time-step interval used in the MD simulation.
  Default: 1.0 * fs

• reservoir_temperature (PhysicalQuantity of type temperature | list) – The reservoir temperature in the simulation.
  Default: 300.0 * Kelvin

• thermostat_timescale (PhysicalQuantity of type time) – The time constant for Berendsen temperature coupling.
  Default: 100.0 * fs

• reservoir_pressure (PhysicalQuantity of type pressure) – The reservoir pressure in the simulation. The pressure can be given either as a scalar value, as a vector of length 3 denoting the hydrostatic components, as a vector of length 6 in Voigt notation, or as a 3x3 tensor. A scalar value will result in isotropic pressure coupling, whereas for all other representations, each pressure component will be coupled to the barostat independently.
  Default: 1.0*bar

• barostat_timescale (PhysicalQuantity of type time) – The time constant for Berendsen pressure coupling.
  Default: 1000.0 * fs

• compressibility (PhysicalQuantity of type pressure**-1) – The estimated compressibility of the system relating volume changes to pressures changes.
  Default: 1.0e-4*bar**-1

• coupling_mask (array of bools) – The mask determining which elements of the stress tensor, the barostat should couple to. Can be given as a vector of length 3, denoting the hydrostatic components, as a vector of length 6 in Voigt notation, or as a 3x3 tensor. By default the barostat couples only to the diagonal elements.
  Default: True for diagonal elements, False for shear components.

• heating_rate (PhysicalQuantity of type temperature/time | None) – The heating rate of the target temperature. A value of None disables the heating of the system.
  Default: None

• compression_rate (PhysicalQuantity of type pressure/time | None) – The compression rate of the target pressure.
  Default: 0.0 * bar/fs

• random_seed (int) – The seed for the random generator providing the stochastic part of the velocity scaling. Must be between 0 and 2**32.
  Default: The default random seed

isotropicCoupling()

Returns:

Whether the barostat applies isotropic or anisotropic pressure coupling.

Return type:

bool

kineticEnergy(configuration)

Parameters:

configuration (DistributedConfiguration) – The current configuration to calculate the kinetic energy of.

Returns:

The kinetic energy of the current configuration.

Return type:

PhysicalQuantity of type energy

thermostats()

Returns:

The list of thermostats.

Return type:

list

timeStep()

Returns:

The time step.

Return type:

PhysicalQuantity of type time

uniqueString()

Return a unique string representing the state of the object.

Usage Example

Perform a molecular dynamics run of 50 steps on FCC Si in the isothermal-isobaric ensemble using the NPTBernettiBussi method:

# Set up configuration
bulk_configuration = BulkConfiguration(
    bravais_lattice=FaceCenteredCubic(5.4306*Angstrom),
    elements=[Silicon, Silicon],
    fractional_coordinates=[[0.0, 0.0, 0.0], [0.25, 0.25, 0.25]]
    )

# Set calculator
calculator = TremoloXCalculator(parameters=Tersoff_Si_1988b())
bulk_configuration.setCalculator(calculator)

# Set up MD method
method = NPTBernettiBussi(
    time_step=1*femtoSecond,
    initial_velocity=MaxwellBoltzmannDistribution(temperature=300*Kelvin),
    # Thermostat settings
    reservoir_temperature=300*Kelvin,
    thermostat_timescale=100*femtoSecond,
    heating_rate=0*Kelvin/picoSecond,
    # Barostat settings
    reservoir_pressure=1.0*bar,
    barostat_timescale=1000.0*femtoSecond,
    compressibility=1.0e-4*bar**-1,
)

# Run MD simulation
md_trajectory = MolecularDynamics(
    bulk_configuration,
    constraints=[],
    trajectory_filename='trajectory.hdf5',
    steps=50,
    log_interval=10,
    method=method
)

nptbernettibussi.py

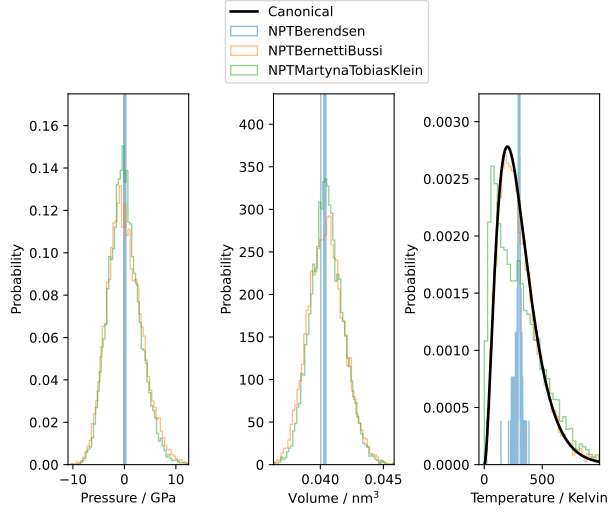
The Bernetti-Bussi thermostat combines the stochastic velocity rescaling thermostat [1] for temperature controll with the stochastic cell rescaling barostat [2] for pressure control. It correctly produces the volume and temperature distributions of the NPT ensemble.

The script below compares the (instantaneous) pressure, volume and temperature distributions generated by three different barostats: Both the Martyna-Tobias-Klein (MTK) barostat and the Bernetti-Bussi barostat give the correct broad volume and huge pressure fluctuations, while the Berendsen barostat produces a very narrow distribution.

Since the center of mass is constrained, the system has only 3 degrees of freedom. The deterministic MTK method has difficulties in reaching the canonical distribution for the instantaneous temperature on such a small system.

compare_PVT_distributions.py

Notes

• The Bernetti-Bussi barostat [2], [3] is a stochastic variant of the Berendsen barostat. However, unlike the Berendsen barostat it correctly samples the isothermal-isobaric ensemble. The lattice vectors of the cell and the positions are scaled by a random number, which is chosen such as to achieve the correct volume fluctuations.

• If a scalar reservoir_pressure value is given, isotropic pressure coupling is applied, i.e. all cell vectors are rescaled by the same factor, and the isotropic pressure \(P=1/3 (P_{xx} + P_{yy} + P_{zz})\) is used.

  If a pressure vector (of length 3 or 6, in Voigt notation), or a 3x3-tensor is given as reservoir_pressure, anisotropic pressure coupling is applied, meaning that each degree of freedom of the cell vectors will be rescaled independently.

The coupling to selected components of the pressure tensor can be enabled/disabled via the parameter coupling_matrix. This parameter only has an effect with anisotropic pressure coupling.

By default, the barostat couples only to the hydrostatic pressure, i.e. the diagonal elements of the pressure tensor.

• If a non-zero heating_rate is specified, the reservoir temperature will be changed linearly during the simulation, according to the specified heating rate.

  If a non-zero compression_rate is specified, the reservoir pressure will be changed linearly during the simulation, according to the specified compression rate.

[1]

Giovanni Bussi, Davide Donadio, and Michele Parrinello. Canonical sampling through velocity rescaling. Journal of Chemical Physics, 126(1):014101, 2007. doi:10.1063/1.2408420.

[2] (1,2)

Mattia Bernetti and Giovanni Bussi. Pressure control using stochastic cell rescaling. The Journal of chemical physics, 153 11:114107, 2020.

[3]

Vittorio Del Tatto, Paolo Raiteri, Mattia Bernetti, and Giovanni Bussi. Molecular Dynamics of Solids at Constant Pressure and Stress Using Anisotropic Stochastic Cell Rescaling. Applied Sciences, 2022.