SemiCircleContour¶
- class SemiCircleContour(integral_lower_bound=None, circle_eccentricity=None, logarithmic_bunching=None, circle_points=None, fermi_line_points=None, fermi_function_poles=None)¶
An equilibrium contour using the semi-circle contour points and weights defined in [1].
- Parameters:
integral_lower_bound (PhysicalQuantity of type energy) – The distance between the lowest Fermi-level and the lowest energy circle contour point. Default: An energy determined on the chosen pseudopotentials or 1.5 Hartree for the semi-empirical calculators.
circle_eccentricity (float) – The eccentricity of the circle contour. This should be a float between 0 and 1. 0 is a circle, 1 is a line. Default:
0.3logarithmic_bunching (float) – Logarithmic bunching of the circle contour around the Fermi level. This should be a float between 0 and 1. 0 means no bunching, equidistant points, 1 means all bunched, centred on the Fermi Level. Default:
0.3circle_points (int > 2) – The number of points on the circle contour. Default:
30fermi_line_points (int) – The number of points on the straight line from the Fermi energy level up to infinity. This should be an integer in the range 1 to 11 (inclusive). Default:
10fermi_function_poles (int > 0) – The number of poles of the Fermi function to include. Determines the imaginary shift of the straight line from the Fermi level to infinity. Default:
8
- circleEccentricity()¶
- Returns:
The eccentricity of the circle contour.
- Return type:
float
- circlePoints()¶
- Returns:
The number of circle points.
- Return type:
int
- fermiFunctionPoles()¶
- Returns:
The number of poles for the Fermi function.
- Return type:
int
- fermiLinePoints()¶
- Returns:
The number of points on the line from the Fermi energy level up to infinity.
- Return type:
int
- integralLowerBound()¶
- Returns:
The distance between the lowest Fermi-level to the lowest energy circle contour point.
- Return type:
PhysicalQuantity of type energy
- logarithmicBunching()¶
- Returns:
The logarithmic bunching.
- Return type:
float
- nlinfo()¶
- Returns:
The nlinfo.
- Return type:
dict
- uniqueString()¶
Return a unique string representing the state of the object.
Usage Example¶
One can use the SemiCircleContour by defining it as an equilibrium contour
equilibrium_contour = SemiCircleContour()
which constructs a SemiCircleContour with all defaults. Alternatively, more parameters that alter the accuracy of the approximation can be specified, e.g.
equilibrium_contour = SemiCircleContour(
circle_eccentricity=0.1,
logarithmic_bunching=0.2,
circle_points=100,
fermi_line_points=11,
fermi_function_poles=10)
To use it in a calculation of the equilibrium density matrix,
the equilibrium contour explicitly on the ContourParameters object,
the EquilibriumContour object is passed to the ContourParameters object,
contour_parameters = ContourParameters(equilibrium_contour=equilibrium_contour)
and saved on the calculator
device_calculator = DeviceLCAOCalculator(contour_parameters=contour_parameters)
Notes¶
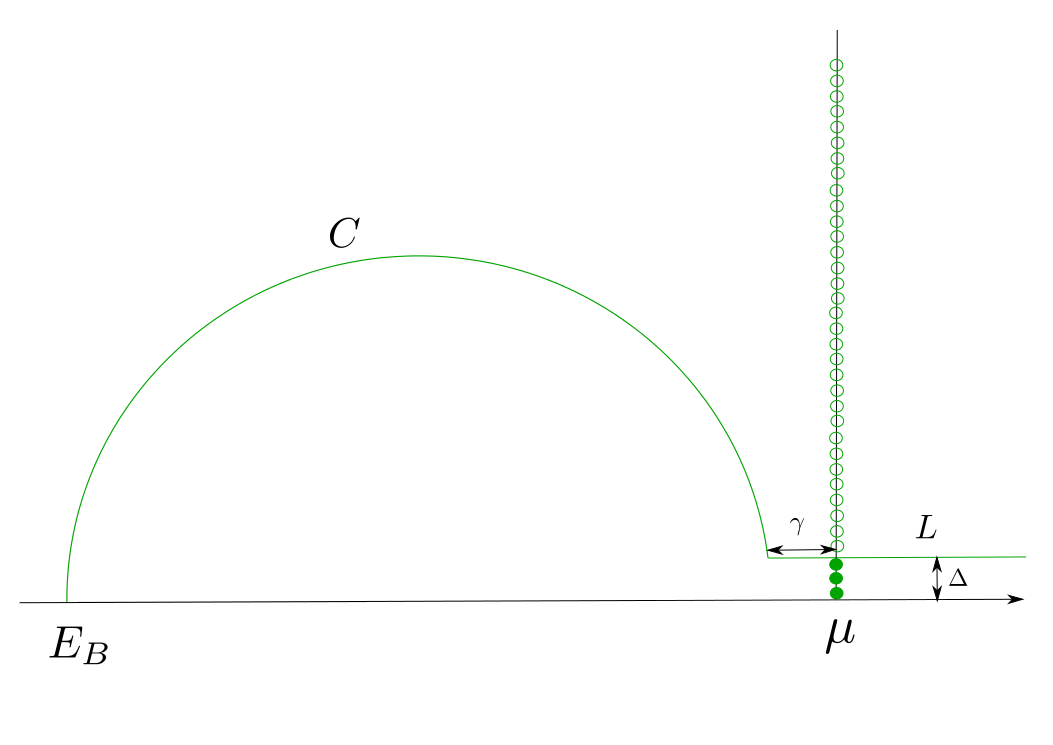
The SemiCircleContour is a method to calculate the equilibrium density matrix \(D\) by performing an integration of the Greens Function \(G\).
in which \(f(E)\) is the Fermi-Dirac distribution and \(\mu\) the Fermi level.
This integral can be solved by using the residue theorem:
in which the sum on the right hand side runs over the poles of the integrant included in the contour.
The SemiCircleContour defines the contour in the upper-half of the imaginary plane and is comprised of a semicircle, a semi-infinite line segment and a finite number of Fermi poles.
The semicircle \(C\) starts from the lower bound \(E_B\)
controlled by integral_lower_bound.
The parameter circle_eccentricity defines the eccentricity of the semi circle,
while adjusting logarithmic_bunching alters the distribution of the semicircle’s
contour points around the fermi level.
The end point of the semicircle is defined at a distance \(\gamma\) below the Fermi energy
\(\mu\) and \(\Delta\) above the real axis.
The line segment \(L\) runs from the semicircle’s end point to \(+\infty\).
The distance \(\Delta\) between the line segment and the real axis is determined
by the number of fermi_poles_poles included in the contour.
The precision of the contour integration improves as
circle_points, the number of contour points on the semicircle,
fermi_line_points, the number of contour points on the line segment,
or fermi_poles_poles increases.
More information about this approach can be found in [1]
