ShockleyReadHallRecombination

class ShockleyReadHallRecombination(charged_point_defect, initial_charge_state, final_charge_state, supercell_repetitions, initial_quantum_numbers, final_quantum_number, fractional_displacements=None, electron_phonon_coupling_configurations=None, electron_phonon_coupling_k_point=None, rotate_to_pure_spin_states=None, supercell_scaling_correction=None, filename=None, object_id=None, number_of_processes_per_task=None, log_filename_prefix=None, save_displaced_configurations=None)

Perform a study of the Shockley-Read-Hall (SRH) recombination between an initial and a final defect charge state.

Parameters:

• charged_point_defect (ChargedPointDefect) – The charged point defect study for which to extract the initial and final charge state from.

• initial_charge_state (int) – The initial charge state of the defect, as a discrete multiple of elementary charge. A charge of -1 corresponds to one extra electron.

• final_charge_state (int) – The final charge state of the defect, as a discrete multiple of elementary charge. A charge of -1 corresponds to one extra electron.

• supercell_repetitions (sequence (size 3) of int) – The supercell of the (charge point defect study) bulk unit cell given as the number of repetitions of the bulk unit cell along the (a, b, c) directions.

• initial_quantum_numbers (sequence of int (nonnegative)) – The quantum numbers for the initial states contributing to the calculation of the electron-phonon coupling matrix element.

• final_quantum_number (int (nonnegative)) – The quantum number for the final state in the calculation of the electron-phonon coupling matrix element.

• fractional_displacements (sequence of float) – The fractional displacements from the center displacement configuration in terms of the generalized configuration coordinate delta. Both the initial and final charge state configuration will be the center displacement configuration.
  Default: [-0.02, -0.01, 0.0, 0.01, 0.02]

• electron_phonon_coupling_configurations (InitialChargeState | FinalChargeState | [InitialChargeState, FinalChargeState]) – Determine whether the configuration used to evaluate the electron-phonon coupling matrix element is the initial charge state configuration or the final charge state configuration or that both can be evaluated.
  Default: [InitialChargeState, FinalChargeState]

• electron_phonon_coupling_k_point (list(3) of floats) – The k-point of the electronic states used to evaluate the electron phonon coupling matrix element, in fractional coordinates.
  Default: The k-point from the configuration calculator if only one k-point is present, [0.0, 0.0, 0.0]

• rotate_to_pure_spin_states (bool) – Boolean to control if the eigenstates should be rotated to pure spin states or not when evaluating the electron-phonon coupling matrix elements. This is only relevant for non-collinear or spin-orbit calculations.
  Default: True

• supercell_scaling_correction (Disabled | ShockleyReadHallSupercellScalingCorrection) – Specifies the parameters for calculating the scaling factor for the interaction between the defect and the bulk wavefunction when the defect has a finite charge. Disabled means no scaling factors are calculated.
  Default: Disabled

• filename (str) – The full or relative filename path the Study object should be saved to. See nlsave().
  Default: The file name of the input charge point defect study.

• object_id (str) – The name of the study that the study object should be saved to within the file. This needs to be a unique name in this file.
  Default: 'srh_recombination_' + initial_charge_state + '_' + final_charge_state

• number_of_processes_per_task (int | ProcessesPerNode) – The number of processes that will be used to execute each task. If the total number of processes does not divide evenly into the tasks, some tasks may have less than this number of processes.
  Default: AllProcesses, all available processes execute each task collaboratively.

• log_filename_prefix (str | LogToStdOut) – Filename prefix for the logging output of SRH recombination study. If LogToStdOut, all logging will instead be sent to standard output.
  Default: 'srhrecombination_'

• save_displaced_configurations (bool) – Whether the displaced updated configuration used to determine the total energies should be saved to disk. If True, they can be inspected or reused, possibly saving computational time if running again the study, or if shared with other studies. However the file where the study is saved will be significantly larger.
  Default: False

calculateCaptureCoefficient(temperature=None, degeneracy_factor=None, charge_state_id=None, initial_quantum_numbers=None, gaussian_broadening=None, sommerfeld_temperature_scaling_factor=None, effective_mass=None, dielectric_constant=None, include_supercell_scaling_factor=None, spin=None)

Calculate the capture coefficient.

Parameters:

• temperature – The temperature(s) at which the capture coefficient is evaluated.
  Default: 300 * Kelvin

• degeneracy_factor (int) – The configurational degeneracy of the final state.
  Default: 1

• charge_state_id (InitialChargeState | FinalChargeState) – Determine whether the configuration used to evaluate the electron-phonon coupling matrix element is the initial charge state configuration or the final charge state configuration.
  Default: If the electron phonon coupling is only calculated for one configuration, use the one available configuration. Otherwise use FinalChargeState.

• initial_quantum_numbers (sequence of int (nonnegative)) – The quantum numbers for the initial states contributing to the calculation of the electron-phonon coupling matrix element. Note that root sum square of all contributions from individual initial quantum numbers is used.
  Default: All available initial quantum numbers.

• gaussian_broadening (PhysicalQuantity of type energy) – The standard deviation of the gaussian broadening used instead of a delta function in the phonon selection rules.
  Default: the final state oscillator energy.

• sommerfeld_temperature_scaling_factor (Analytical | Numerical | Disabled) – Whether the temperature scaling via inclusion of the Sommerfeld parameter should be considered, and if so whether the analytical or numerical expression should be used.
  Default: Disabled

• effective_mass (PhysicalQuantity of type mass.) – The effective mass of the carrier. Only used if sommerfeld_scaling_factor is not Disabled.
  Default: 1 * electron_mass

• dielectric_constant (float) – The relative dielectric constant of the host material. Only used if sommerfeld_scaling_factor is not Disabled.
  Default: The value provided in the charged point defect.

• include_supercell_scaling_factor (bool) – If True, the squared electron-phonon coupling is multiplied by a supercell scaling factor which corrects for distortion in the bulk state due to attractive or repulsive interaction with the localized charged defects state.
  Default: True.

• spin (Spin.Up | Spin.Down) – The spin component to calculate the electron-phonon matrix element for. Only used for polarized. For non-collinear and spin-orbit Spin.All is returned.

static calculateCaptureCoefficientFromParameters(supercell_volume, generalized_configuration_coordinate_delta, energy_difference, electron_phonon_coupling, initial_state_effective_vibration_frequency, final_state_effective_vibration_frequency, degeneracy_factor=1, temperature=PhysicalQuantity(300.0, K), gaussian_broadening=None, sommerfeld_temperature_scaling_factor=None, defect_charge_ratio=-1, effective_mass=PhysicalQuantity(1.0, me), dielectric_constant=1.0)

Utility to calculate the capture coefficient using raw physical parameters as input.

Parameters:

• supercell_volume (PhysicalQuantity of type volume.) – The volume of the defect supercell.

• generalized_configuration_coordinate_delta (PhysicalQuantity of type sqrt(mass) * length) – The displacement between the initial and final state in generalized configuration coordinates.

• energy_difference (PhysicalQuantity of type energy.) – The energy difference between excited state and ground state, i.e. the distance between valence band edge and transition state level for hole recombination or the distance between the transition state level and conduction band edge for electron recombination.

• electron_phonon_coupling (PhysicalQuantity of type energy / sqrt(mass) / length) – The electron-phonon coupling between the initial and final state.

• initial_state_effective_vibration_frequency (PhysicalQuantity of type frequency) – The effective frequency of the harmonic oscillator associated with the initial state.

• final_state_effective_vibration_frequency (PhysicalQuantity of type frequency) – The effective frequency of the harmonic oscillator associated with the final state.

• degeneracy_factor (PhysicalQuantity of type temperature | array of PhysicalQuantity of type temperature) – The configurational degeneracy of the final state.
  Default: 1

• temperature – The temperature(s) at which the capture coefficient is evaluated.
  Default: 300 * Kelvin

• gaussian_broadening (PhysicalQuantity of type energy) – The standard deviation of the gaussian broadening used instead of a delta function in the phonon selection rules.
  Default: the final state oscillator energy.

• sommerfeld_temperature_scaling_factor (Analytical | Numerical | Disabled) – Whether the temperature scaling via inclusion of the Sommerfeld parameter should be considered, and if so whether the analytical or numerical expression should be used.
  Default: Disabled

• defect_charge_ratio (float) – The ratio between the defect charge (before recombination, i.e. the initial charge state), and the carrier charge. Only used if sommerfeld_scaling_factor is not Disabled.

• effective_mass (PhysicalQuantity of type mass.) – The effective mass of the carrier. Only used if sommerfeld_scaling_factor is not Disabled.
  Default: 1 * electron_mass

• dielectric_constant (float) – The relative dielectric constant of the host material. Only used if sommerfeld_scaling_factor is not Disabled.
  Default: 1.0

calculateEffectiveVibrationFrequency(charge_state_id)

Calculate the effective vibration frequency of the charge state.

Parameters:

charge_state_id (InitialChargeState | FinalChargeState) – The charge state for which the effective vibration frequency is calculated.

Returns:

The frequency of the effective phonon mode associated with the given charge state, evaluate by quadratic fit of the total energy as a function of the displacement in generalized configuration coordinates.

Type:

PhysicalQuantity of type frequency.

calculateElectronPhononCouplingMatrixElement(initial_quantum_number, charge_state_id, spin=None)

Calculate the electron-phonon coupling matrix element.

Parameters:

• initial_quantum_number (int) – The quantum number of the bulk-like state for which the electron-phonon coupling is calculated.

• charge_state_id (InitialChargeState | FinalChargeState) – Determine whether the configuration used to evaluate the electron-phonon coupling matrix element is the initial charge state configuration or the final charge state configuration.

• spin (Spin.Up | Spin.Down | Spin.All) – The spin component to calculate the matrix element for. Only used for polarized. For non-collinear and spin-orbit Spin.All is returned.
  Default: Spin.Up

Returns:

The electron-phonon coupling matrix element.

Return type:

PhysicalQuantity of type energy over length square root mass.

chargedPointDefect()

Returns:

The charged point defect study from which the initial and final charge state is extracted from.

Return type:

ChargedPointDefect

configurationCoordinateDelta()

Returns:

The calculated change in the configuration coordinate. If not available, returns None.

Return type:

PhysicalQuantity of type length | None

dependentStudies()

Returns:

The list of dependent studies.

Return type:

list of Study

displacedConfigurationGeneralizedConfigurationCoordinate(charge_state_id, fractional_displacement)

Retrieve the generalized configuration coordinate for the displaced configuration.

Parameters:

• charge_state_id (InitialChargeState | FinalChargeState) – The charge state of the center displacement configuration from which the displaced configuration is displaced from. Either the charge state of the initial configuration or the final configuration.

• fractional_displacement (float) – The fragment displacement from the center displacement configuration. Must be among the fractional displacements.

Returns:

The generalized configuration coordinate for the displaced configuration. If not available, returns None.

Return type:

PhysicalQuantity of type length square root mass | None

displacedConfigurationTotalEnergy(charge_state_id, fractional_displacement)

Retrieve the total energy for the displaced configuration.

Parameters:

• charge_state_id (InitialChargeState | FinalChargeState) – The charge state of the center displacement configuration from which the displaced configuration is displaced from. Either the charge state of the initial configuration or the final configuration.

• fractional_displacement (float) – The fragment displacement from the center displacement configuration. Must be among the fractional displacements.

Returns:

The calculated total energy analysis object for the displaced configuration. If not available, returns None.

Return type:

TotalEnergy | None

electronPhononCouplingConfigurations()

Returns:

A list of flags identifying the charge state configurations for which the electron-phonon coupling matrix element can be evaluated.

Return type:

list of InitialChargeState and/or FinalChargeState

electronPhononCouplingKPoint()

Returns:

The k-point of the electronic states used to evaluate the electron phonon coupling matrix element, in fractional coordinates.

Return type:

list(3) of floats

filename()

Returns:

The filename where the study object is stored.

Return type:

str

finalChargeState()

Returns:

The final charge state of the defect, as a discrete multiple of elementary charge. A charge of -1 corresponds to one extra electron.

Return type:

int

finalQuantumNumber()

Returns:

The quantum number for the final state in the calculation of the electron-phonon coupling matrix element.

Return type:

int (nonnegative)

fractionalDisplacements()

Returns:

The fractional displacements from the center displacement configuration in terms of the generalized configuration coordinate delta.

Return type:

sequence of float

generalizedConfigurationCoordinateDelta()

Returns:

The calculated change in the generalized configuration coordinate. If not available, returns None.

Return type:

PhysicalQuantity of type length square root mass | None

huangRhysFactor(charge_state_id)

Evaluate the dimensionless Huang-Rhys factor for the effective vibrational mode associated with a given charge state:

\[S_{i, f} = \frac{1}{2\hbar}(\Delta Q)^2 \Omega_{i, f}\]

Parameters:

charge_state_id (InitialChargeState | FinalChargeState) – The charge state for which the Huang-Rhys factor is calculated.

Returns:

The calculated Huang-Rhys factor. If not available yet, returns None.

Return type:

float | None

initialChargeState()

Returns:

The initial charge state of the defect, as a discrete multiple of elementary charge. A charge of -1 corresponds to one extra electron.

Return type:

int

initialQuantumNumbers()

Returns:

The quantum numbers for the initial states contributing to the calculation of the electron-phonon coupling matrix element.

Return type:

sequence of int (nonnegative)

logFilenamePrefix()

Returns:

The filename prefix for the logging output of the study.

Return type:

str | LogToStdOut

nlinfo()

Returns:

Structured information about the Study.

Return type:

dict

nlprint(stream=None)

Print a string containing an ASCII table useful for plotting the Study object.

Parameters:

stream (python stream) – The stream the table should be written to.
Default: NLPrintLogger()

numberOfProcessesPerTask()

Returns:

The number of processes to be used to execute each task. If None, all available processes execute each task collaboratively.

Return type:

int | None | ProcessesPerNode

numberOfProcessesPerTaskResolved()

Returns:

The number of processes to be used to execute each task. Default values are resolved based on the current execution settings.

Return type:

int

objectId()

Returns:

The name of the study object in the file.

Return type:

str

rotateToPureSpinStates()

Returns:

Whether the eigenstates should be rotated to pure spin states or not when evaluating the electron-phonon coupling matrix elements.

Return type:

bool

saveDisplacedConfigurations()

Returns:

Whether the displaced configurations should be saved.

Return type:

bool

saveToFileAfterUpdate()

Returns:

Whether the study is automatically saved after it is updated.

Return type:

bool

spins()

Returns:

The available spin components.

Return type:

list of Spin.Up | Spin.Down | Spin.All

supercellRepetitions()

Returns:

The supercell of the (charge point defect study) bulk unit cell given as the number of repetitions of the bulk unit cell along the (a, b, c) directions.

Return type:

sequence (size 3) of int

supercellScalingCorrection()

Returns:

Specifies the parameters for calculating the scaling factor for the interaction between the defect and the bulk wavefunction when the defect has a finite charge. Disabled means no scaling factors are calculated.

Return type:

ShockleyReadHallSupercellScalingCorrection

supercellScalingCorrectionFactors(charge_state_id, spin=None)

Retrieve the supercell scaling correction factors.

Parameters:

• charge_state_id (InitialChargeState | FinalChargeState) – The charge state configuration for which the supercell scaling correction factors is retrieved.

• spin (Spin.Up | Spin.Down | Spin.All) – The spin component to extract the scaling factors for.
  Default: Spin.Up

Returns:

Retrieve the supercell scaling correction factors as a list. If not available, returns None.

Return type:

list of float | None

uniqueString()

Return a unique string representing the state of the object.

update()

Run the calculations for the study object.

updatedDisplacedConfiguration(charge_state_id, fractional_displacement)

Retrieve the updated displaced configuration, if available.

Parameters:

• charge_state_id (InitialChargeState | FinalChargeState) – The charge state of the center displacement configuration from which the displaced configuration is displaced from. Either the charge state of the initial configuration or the final configuration.

• fractional_displacement (float) – The fragment displacement from the center displacement configuration. Must be among the fractional displacements.

Returns:

The updated displaced configuration. If not available, returns None.

Return type:

BulkConfiguration | None

wavefunctionOverlapsAndEnergyDifferences(charge_state_id, fractional_displacement)

Retrieve the wavefunction overlaps and energy differences.

Parameters:

• charge_state_id (InitialChargeState | FinalChargeState) – The configuration for which the overlap integrals and energy differences for the evaluation of electron-phonon coupling have been calculated.

• fractional_displacement (float) – The fragment displacement from the center displacement configuration. Must be among the fractional displacements.

Returns:

Retrieve the wavefunction overlaps and energy differences as a container object. If not available, returns None.

Return type:

WavefunctionOverlapsAndEnergyDifferences | None

Notes

The ShockleyReadHallRecombination study object allows to calculate the capture rate associated to a Shockley-Read-Hall (SRH) non-radiative recombination mediated by a trap state, following the the methodology developed by Alkauskas et al. [1].

The carrier capture is characterized by a transition between an initial and a final charge states in a deep level defect, therefore an accurate study of the defect itself is required beforehand.

This analysis can be performed using a ChargedPointDefect, whose results can be in turn used as input quantities to the ShockleyReadHallRecombination study.

Note

A very accurate charged point defect study is required to obtain physical capture rates. In particular, the defect configuration should be relaxed to tight accuracy, and all simulation parameters should be accurately chosen (e.g. exchange-correlation functional) and well converged.

The ShockleyReadHallRecombination object performs 3 main operations:

• Total energy analysis of the charge state configurations in generalized configuration coordinates, to determine the vibrational properties of the system.

• Evaluation of electron-phonon coupling matrix elements between the carrier bulk states and the defect trap state.

• Post-processing to evaluate capture rates based on those quantities.

Choice of initial and final charge state

The ShockleyReadHallRecombination requires information about the initial and final defect charge states involved in the carrier capture, specified in the input parameters initial_charge_state and final_charge_state. For example, the process of capturing a hole by a ionized defect state with a transition level 0/-1 in gap is identified by initial_charge_state=-1 and final_charge_state=0. Hence, the choice of those parameters is dictacted by the process which must be simulated and the defect transition state levels available for that process.

Choice of initial and final quantum numbers

In order to calculate the capture rate, the electron-phonon coupling matrix element between the initial bulk-like carrier state and the final localized trap state must be evaluated. To this end, Kohn-Sham states from the defect configuration are utilized. In particular, knowledge of the quantum number of a state representative of a localized defect state in gap, and of the quantum numbers of the initial bulk-like states, are required.

Unluckily, there is no automated way to determine those states, and some inspection of the ChargedPointDefect is required. For each charge state it should be inspected whether a localized state in gap exists. If this is the case, the corresponding quantum number can be selected as final_quantum_number. The bulk-like states will be specified using the parameter initial_quantum_numbers. In principle, both the initial and final charge state configurations can be used, as long as a well distinguished localized defect state in gap is present. However, a neutral charge state configuration (if any) should be preferred, since it will circumvent artifacts due to the finite supercell size.

An example of how such parameters can be determined is given in the section below, and a theoretical discussion can be found in ref. [1].

Scaling factors

The nominal capture rate is determined as in equation 22 in ref. [1]. This quantity can be scaled to take into account temperature effects and supercell size effects. The former scaling factor is introduced when evaluating the capture rate through the method calculateCaptureCoefficient(), while the latter is only calculated for non-neutral charge states and requires an extra calculation, controlled by the input parameter supercell_scaling_correction.

The temperature scaling is determined as described in reference [2], while the evaluation of the supercell scaling correction follows the methodology implemented in Nonrad by by Turianski et al. [3]. By definition, the supercell scaling correction is set to 1 for the neutral charge state.

Usage example

This example performes a study of hole capture rate in Gallium Nitride with Carbon substitutional defects. The calculation runs in about one day on a single node with 40 cores, and calculation parameters have been chosen to trade off accuracy and execution time. Results for the same type of capture mechanism are reported in [1], [3], but please note that for a meaningful comparison consistent simulation parameters should be chosen.

First, the charged point defect is evaluated as in the script below. A MGGA.SCAN functional is used for geometry relaxations and formation energy calculations. The transition state levels are corrected using an HybridGGA.HSE functional. Such combination provides results comparable with literature at a fraction of the execution time which would be required for a full calculation using hybrid functional. Optimization parameters tighter than the default will be required to evaluate reliably the vibrational properties.

The ChargedPointDefect can include multiple charge states, in this case we know beforehand that we are interested in the charge states -1 and 0.

# -*- coding: utf-8 -*-
setVerbosity(MinimalLog)

# -------------------------------------------------------------
# Bulk Configuration
# -------------------------------------------------------------

# Set up lattice
lattice = SimpleOrthorhombic(5.546690740087016*Angstrom, 3.2093295699579034*Angstrom, 5.241822783047967*Angstrom)

# Define elements
elements = [Gallium, Gallium, Nitrogen, Nitrogen, Gallium, Gallium, Nitrogen,
            Nitrogen]

# Define coordinates
fractional_coordinates = [[ 0.338086773247, -0.            ,  0.005917824105],
                          [ 0.661913226753,  0.            ,  0.505917824105],
                          [ 0.329542526042,  0.            ,  0.379082175895],
                          [ 0.670457473958, -0.            ,  0.879082175895],
                          [ 0.838086773247,  0.5           ,  0.005917824105],
                          [ 0.161913226753,  0.5           ,  0.505917824105],
                          [ 0.829542526042,  0.5           ,  0.379082175895],
                          [ 0.170457473958,  0.5           ,  0.879082175895]]

# Set up configuration
bulk_configuration = BulkConfiguration(
    bravais_lattice=lattice,
    elements=elements,
    fractional_coordinates=fractional_coordinates
    )

# -------------------------------------------------------------
# Calculator
# -------------------------------------------------------------
#----------------------------------------
# Exchange-Correlation
#----------------------------------------
exchange_correlation = MGGA.SCAN

basis_set = [
    BasisGGAPseudoDojo.Nitrogen_Medium,
    BasisGGAPseudoDojo.Gallium_Medium,
    BasisGGAPseudoDojo.Carbon_Medium,
    ]

k_point_sampling = KpointDensity(
    density_a=4.0*Angstrom,
    )
numerical_accuracy_parameters = NumericalAccuracyParameters(
    density_mesh_cutoff=95.0*Hartree,
    k_point_sampling=k_point_sampling,
    )

calculator = LCAOCalculator(
    exchange_correlation=MGGA.SCAN,
    basis_set=basis_set,
    numerical_accuracy_parameters=numerical_accuracy_parameters,
    )

bulk_configuration.setCalculator(calculator)
nlprint(bulk_configuration)
bulk_configuration.update()
nlsave('charge_point_defect.hdf5', bulk_configuration)

# -------------------------------------------------------------
# Charged Point Defect
# -------------------------------------------------------------
# Defect
point_defect = Substitutional(
    element=Carbon,
    site_index=2,
    unit_cell_index=(0, 0, 0))

# Charge states
charge_states = [-1, 0]

# Atomic chemical potentials
atomic_chemical_potentials = [
    AtomicChemicalPotential(element=Carbon, internal_energy=None),
    AtomicChemicalPotential(element=Nitrogen, internal_energy=None)
]

# Supercell repetitions
supercell_repetitions_list = [
    [2, 3, 2],
]

# File name.
filename = 'charge_point_defect.hdf5'

band_gap_calculator = calculator(exchange_correlation=HybridGGA.HSE06)

charged_point_defect = ChargedPointDefect(
    bulk_configuration=bulk_configuration,
    formation_energy_calculator=calculator,
    band_gap_calculator=band_gap_calculator,
    filename=filename,
    object_id='charged_point_defect',
    point_defect=point_defect,
    charge_states=charge_states,
    atomic_chemical_potentials=atomic_chemical_potentials,
    supercell_repetitions_list=supercell_repetitions_list,
    relax_atomic_coordinates=True,
    dielectric_constant=8.9,
    log_filename_prefix='charged_point_defect_',
    number_of_processes_per_task=None,
    elastic_correction_method=None,
    optimize_geometry_parameters=OptimizeGeometryParameters(max_forces=0.01*eV/Angstrom),
    random_seed=1
)
charged_point_defect.update()

charged_point_defect.py

Once the calculation is completed, we can verify in the labfloor that the transition level (-1/0) is located at 1.03 eV above Valence band, in agreement with reported computational results.

Before setting up the ShockleyReadHallRecombination object, we inspect the charged point defect to determine the electronic quantum numbers required to evaluate the electron-phonon coupling matrix element. To this end, we evaluate the ElectronicInverseParticipationRatio (IPR), which gives an indication of the degree of eigenstate localization in the system.

The following snippet extracts the configurations from the charged point defect study and calculated the IPR for both charge states.

from SMW import *

cpd = nlread('charged_point_defect.hdf5', ChargedPointDefect)[-1]

defect_configuration = cpd.defectConfiguration(
    (2, 3, 2),
    charge_state=0)

ipr = ElectronicInverseParticipationRatio(defect_configuration)
nlsave('defect_configuration_0.hdf5', ipr)

defect_configuration = cpd.defectConfiguration(
    (2, 3, 2),
    charge_state=-1)

ipr = ElectronicInverseParticipationRatio(defect_configuration)
nlsave('defect_configuration_-1.hdf5', ipr)

ipr_evaluation.py

The result can be visualized on the labfloor, a plot like the one below is visualized:

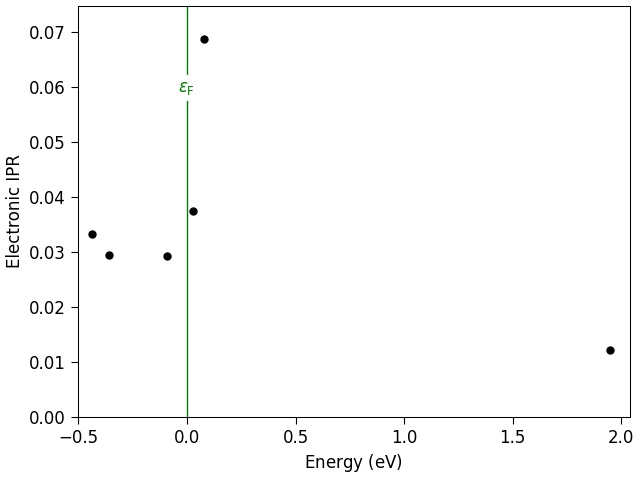
Fig. 171 Electronic Inverse Participation Ratio for the neutral charge state.

We identify a strongly localized state in gap. The state on the right corresponds to the conduction band edge, while the states below the localized one are bulk-like states, partially localized by the interaction with the defect. The ElectronicInverseParticipationRatio allows us to identify the defect state with the quantum number 431, and as bulk-like states we choose the three states below, since in the ideal bulk the recombination would involve the three nearly degenerate top valence bands.

Note

A FatBandstructure with projection on the defect site a and BlochState for visual inspection can be utilized to further inspect the Kohn-Sham states and decide whether a localized defect state can be identified.

In this specific case, we could identify the defect and bulk-like states in the neutral charge state configuration.

Once this preliminary analysis of the charged point defect is done, we can setup and run the ShockleyReadHallRecombination object as shown in the script below.

from SMW import *

charged_point_defect = nlread('charged_point_defect.hdf5', ChargedPointDefect)[-1]

initial_quantum_numbers = [430, 429, 428]
final_quantum_number = 431

srh = ShockleyReadHallRecombination(
    charged_point_defect,
    initial_charge_state=-1,
    final_charge_state=0,
    supercell_repetitions=charged_point_defect.supercellRepetitionsList()[-1],
    initial_quantum_numbers=initial_quantum_numbers,
    final_quantum_number=final_quantum_number,
    fractional_displacements=[-0.05, -0.025, 0., 0.025, 0.05],
    object_id='srh-medium-scan-hse',
    filename='shockley_read_hall.hdf5',
    log_filename_prefix='shockley_read_hall')

srh.update()

shockley_read_hall.py

The results can be inspected using nlprint, as shown below, or the getters implemented on the object.

+------------------------------------------------------------------------------+
| Shockley-Read-Hall (SRH) Recombination Report                                |
+------------------------------------------------------------------------------+
| Initial charge state:            -1                                          |
| Effective vibration frequency:    5.04e+01  meV                              |
| Huang-Rhys factor:                1.91e+01                                   |
+------------------------------------------------------------------------------+
| Initial quantum number    Electron-phonon coupling    Supercell scaling      |
|                           (eV / Å amu^0.5)            correction             |
| 430                       1.10e-02                    n/a                    |
| 429                       6.84e-03                    n/a                    |
| 428                       6.74e-02                    n/a                    |
+------------------------------------------------------------------------------+
| Final charge state:               0                                          |
| Effective vibration frequency:    5.13e+01  meV                              |
| Huang-Rhys factor:                1.94e+01                                   |
+------------------------------------------------------------------------------+
| Initial quantum number    Electron-phonon coupling    Supercell scaling      |
|                           (eV / Å amu^0.5)            correction             |
| 430                       6.60e-03                    1.00e+00               |
| 429                       2.99e-03                    1.00e+00               |
| 428                       4.00e-02                    1.00e+00               |
+------------------------------------------------------------------------------+
| Final quantum number:                          431                           |
| Generalized configuration coordinate delta:    1.78e+00  Å amu^0.5           |
| Transition state level (from valence band):    1.03e+00  eV                  |
| Supercell volume:                              1.12e+03  Å^3                 |
| Supercell repetitions:                         2 x 3 x 2                     |
+------------------------------------------------------------------------------+

Alternatively, convenience methods can be used to generate plots. _nlplotConfigurationDiagram visualizes the total energy diagram in generalized configuration coordinates, while _nlplotOverlapIntegrals and _nlplotEigenvalueDifferences visualize the components utilized to calculate the electron-phonon coupling matrix element.

# Visualize the configuration coordinate diagram.
srh._nlplotConfigurationDiagram()
# Visualize the overlap integrals for a given charge state.
srh._nlplotOverlapIntegrals(charge_state_id=FinalChargeState)
# Visualize the eigenvalue differences for a given charge state.
srh._nlplotEigenvalueDifferences(charge_state_id=FinalChargeState)

The capture rate can be calculated at different temperaturs using the method calculateCaptureCoefficient(). ShockleyReadHallRecombination implements also a static utility calculateCaptureCoefficientFromParameters() to calculate the capture rate by giving explicitely each physical parameter, e.g. for sensitivity studies or to override some of the parameters obtained from the study object calculation.

[1] (1,2,3,4)

Audrius Alkauskas, Qimin Yan, and Chris G. Van de Walle. First-principles theory of nonradiative carrier capture via multiphonon emission. Phys. Rev. B, 90:075202, Aug 2014. URL: https://link.aps.org/doi/10.1103/PhysRevB.90.075202, doi:10.1103/PhysRevB.90.075202.

[2]

R. Passler. Relationships between the nonradiative multiphonon carrier-capture properties of deep charged and neutral centres in semiconductors. physica status solidi (b), 78(2):625–635, 1976. URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/pssb.2220780222, arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1002/pssb.2220780222, doi:https://doi.org/10.1002/pssb.2220780222.

[3] (1,2)

Mark E. Turiansky, Audrius Alkauskas, Manuel Engel, Georg Kresse, Darshana Wickramaratne, Jimmy-Xuan Shen, Cyrus E. Dreyer, and Chris G. Van de Walle. Nonrad: Computing nonradiative capture coefficients from first principles. Comput. Phys. Commun., 267:108056, October 2021. doi:10.1016/j.cpc.2021.108056.