GrueneisenCoefficient

Included in QATK.Dynamics

class GrueneisenCoefficient(configuration, filename, object_id, calculator=None, cell_displacement_factor=None, dynamical_matrix_parameters=None, optimize_geometry_parameters=None, log_filename_prefix=None, number_of_processes_per_task=None, qpoints=None, include_anisotropy=None)

Calculate the Grueneisen parameter and thermal expansion coefficients.

Parameters:

• configuration (BulkConfiguration) – The configuration for which the Grueneisen coefficient should be calculated.

• filename (str) – The full or relative path to save the results to. See nlsave().

• object_id (str) – The object id to use when saving. See nlsave().

• calculator (Calculators) – The calculator to be used.
  Default: The calculator attached to the configuration.

• cell_displacement_factor (float) – The factor for which the initial configuration cell volume or lattice vectors expands or contracts.
  Default: 0.01

• dynamical_matrix_parameters (DynamicalMatrixParameters) – The DynamicalMatrix parameters.
  Default: DynamicalMatrixParameters().

• optimize_geometry_parameters (OptimizeGeometryParameters) – The parameters for the geometry optimization.

• log_filename_prefix (str | LogToStdOut) – Filename prefix for the logging output. If LogToStdOut, all logging will instead be sent to standard output.
  Default: 'grueneisen_coefficient_'.

• number_of_processes_per_task (int | None | ProcessesPerNode) – The number of processes that will be used to execute each task. If the total number of process does not divide evenly into the tasks, some tasks may have less than this number of processes. If None, all available processes execute each task collaboratively.

• qpoints (sequence (size 3) of int | MonkhorstPackGrid | KpointDensity | RegularKpointGrid) – The q-points for which the mode heat capacities and mode Grueneisen coefficients should be calculated.
  Default: A Monkhorst-Pack grid of size (10, 10, 10).

• include_anisotropy (bool) – Whether to include anisotropic effects in the calculations. If true, the configuration is strained (contracted or expanded) in each lattice direction one at a time and the mode and q-point specific Grueneisen coefficients are determined hereof. If false, the entire configuration volume is expanded and contracted isotropically.
  Default: True

Note

Argument changes:

route

Deprecated since 2026.03

points_per_segment

Deprecated since 2026.03

path

Deprecated since 2026.03

cellDisplacementFactor()

Returns:

The factor for which the initial configuration cell expands or contracts.

Return type:

float

configuration()

Returns:

The initial non-optimized configuration.

Return type:

BulkConfiguration

contractedConfiguration(direction=None)

Return the optimized contracted configuration. Note that this is only applicable after update.

Parameters:

direction (str | None) – The lattice vector direction.

Returns:

The geometry optimized contracted configuration.

Return type:

BulkConfiguration | None

dependentStudies()

Returns:

The list of dependent studies.

Return type:

list of Study

dynamicalMatrixParameters()

Returns:

The parameters for the dynamical matrix.

Return type:

DynamicalMatrixParameters

elasticConstants()

Get the ElasticConstants analysis object from the initial configuration.

Returns:

The ElasticConstants object

Return type:

ElasticConstants | None

expandedConfiguration(direction=None)

Return the optimized expanded configuration. Note that this is only applicable after update.

Parameters:

direction (str | None) – The lattice vector direction.

Returns:

The geometry optimized expanded configuration.

Return type:

BulkConfiguration | None

filename()

Returns:

The filename where the study object is stored.

Return type:

str

grueneisenCoefficient(temperature)

Compute the Grueneisen coefficient at the given temperature.

Parameters:

temperature (PhysicalQuantity in units of temperature) – The temperature condition to consider.

Returns:

The Grueneisen coefficient.

Return type:

float | sequence of shape (3,) of floats

heatCapacity(temperature)

Compute the heat capacity at the given temperature.

Parameters:

temperature (PhysicalQuantity in units of temperature) – The temperature condition to consider.

Returns:

The heat capacity.

Return type:

PhysicalQuantity of type energy per temperature per volume

includeAnisotropy()

Returns:

If anisotropic effects are included or not.

Return type:

bool

linearThermalExpansionCoefficient(temperature)

Compute the linear thermal expansion at the given temperature along a given lattice vector or isotropically depending on the settings.

Parameters:

temperature (PhysicalQuantity in units of temperature) – The temperature condition to consider.

Returns:

The linear thermal expansion coefficient.

Return type:

PhysicalQuantity in units of inverse temperature | Sequence of (3,) PhysicalQuantity in units of inverse temperature

logFilenamePrefix()

Returns:

The filename prefix for the logging output of the study.

Return type:

str | LogToStdOut

nlinfo()

Get only the printable results from the extraction results - plain text.

Returns:

The study information.

Return type:

dict

nlprint(stream=None)

Print a string containing an ASCII table useful for plotting the Study object.

Parameters:

stream (python stream) – The stream the table should be written to.
Default: NLPrintLogger()

numberOfProcessesPerTask()

Returns:

The number of processes to be used to execute each task. If None, all available processes execute each task collaboratively.

Return type:

int | None | ProcessesPerNode

numberOfProcessesPerTaskResolved()

Returns:

The number of processes to be used to execute each task. Default values are resolved based on the current execution settings.

Return type:

int

objectId()

Returns:

The name of the study object in the file.

Return type:

str

optimizeGeometryParameters()

Returns:

The parameters for the geometry optimization.

Return type:

OptimizeGeometryParameters

phononEnergies()

Returns:

The eigenvalues for the phonon band structure. The shape is (Q, B) where Q is the number of q-points and B is the number of bands.

Return type:

PhysicalQuantity of type energy

qpoints()

Get the irreducible q-points.

Returns:

The fractional coordinates of the q-points.

Return type:

numpy.ndarray

saveToFileAfterUpdate()

Returns:

Whether the study is automatically saved after it is updated.

Return type:

bool

uniqueString()

Return a unique string representing the state of the object.

update()

Perform the update. Here, the mode and q point specific Grueneisen coefficients are calculated and used to calculate the temperature dependent part in the thermal expansion coefficient and macroscopic Grueneisen parameter.

volumetricThermalExpansionCoefficient(temperature)

Compute the volumetric thermal expansion at the given temperature.

Parameters:

temperature (PhysicalQuantity in units of temperature) – The temperature condition to consider.

Returns:

The volumetric thermal expansion coefficient.

Return type:

PhysicalQuantity in units of inverse temperature

Usage Examples

Calculate the temperature-dependent Grueneisen coefficient and linear thermal expansion for silicon FCC.

# %% GrueneisenCoefficient

grueneisen_coefficient = GrueneisenCoefficient(
    configuration=bulk_configuration,
    filename='grueneisen_coefficient_example.hdf5',
    object_id='gc',
    include_anisotropy=False,
)
grueneisen_coefficient.update()

print('%15s%30s%30s' % ('Temperature (K)', 'Grueneisen', 'Linear CTE (1/K)'))

temperatures = numpy.linspace(10, 1000, 20) * Kelvin
for temperature in temperatures:
    grueneisen = grueneisen_coefficient.grueneisenCoefficient(temperature)
    linear_thermal_expansion_coefficient = (
        grueneisen_coefficient.linearThermalExpansionCoefficient(temperature)
    )
    print(
        '%15.0f%30.5f%30.5E' % (
            temperature.inUnitsOf(Kelvin),
            grueneisen,
            linear_thermal_expansion_coefficient.inUnitsOf(Kelvin**-1)
        )
    )

grueneisen_coefficient_example.py

Notes

The GrueneisenCoefficient object primarily aims to calculate two properties of a bulk material; the Grüneisen coefficient/parameter and thermal expansion coefficients denoted \(\gamma\) and \(\alpha\), respectively. The thermal expansion coefficient can generally be given either as linear or volumetric, denoted by subscripts \(L\) and \(V\). If a material expands equally in all directions (also called an isotropic material), the following simple relation is valid,

(17)\[\alpha_L = \frac{\alpha_V}{3}\]

The Grüneisen parameter is a dimensionless parameter with several formulations. One widely used relation is,

(18)\[\gamma = \frac{3 \alpha_L B}{C_V}\]

where \(B\) is the Hill bulk modulus obtained from ElasticConstants which is internally computed. \(C_V\) is the heat capacity at constant volume.

The Grüneisen parameter can further be refined into its mode index (\(i\)), q-point and directional (\(L\)) microscopic components denoted \(\gamma_L(\mathbf{q}, i)\).

\[\gamma_L(\mathbf{q}, i) = -\frac{V_0}{2 [h\nu_i(\mathbf{q})]^2} \left\langle \mathbf{e}_i(\mathbf{q}) \middle| \frac{dD_L(\mathbf{q})}{dV_L} \middle| \mathbf{e}_i(\mathbf{q}) \right\rangle\]

Likewise with microscopic \(C_V(\mathbf{q}, i, T)\) which is additionally temperature dependent (\(T\)) and defined as,

\[C_V(\mathbf{q}, i, T) = \frac{[h \nu_i(\mathbf{q})]^2}{V_0 k_B T^2} \frac{\exp{h \nu_i(\mathbf{q})}}{[\exp{h \nu_i(\mathbf{q})} - 1]^2}\]

In the above equations, \(V_0\), \(\mathbf{e}\) and \(\nu\) denote the unit cell volume, phonon system eigenvectors and eigenvalues, respectively, of the initial configuration. \(dD_L(\mathbf{q})\) and \(dV_L\) are the change in q-point specific dynamical matrix (obtained from DynamicalMatrix) and unit cell volume difference, respectively, between the expanded and contracted configurations. In the anisotropic case, expansions and contractions are performed separately in the A, B or C lattice vectors of the unit cell resulting in macroscopic Grüneisen parameters for each direction.

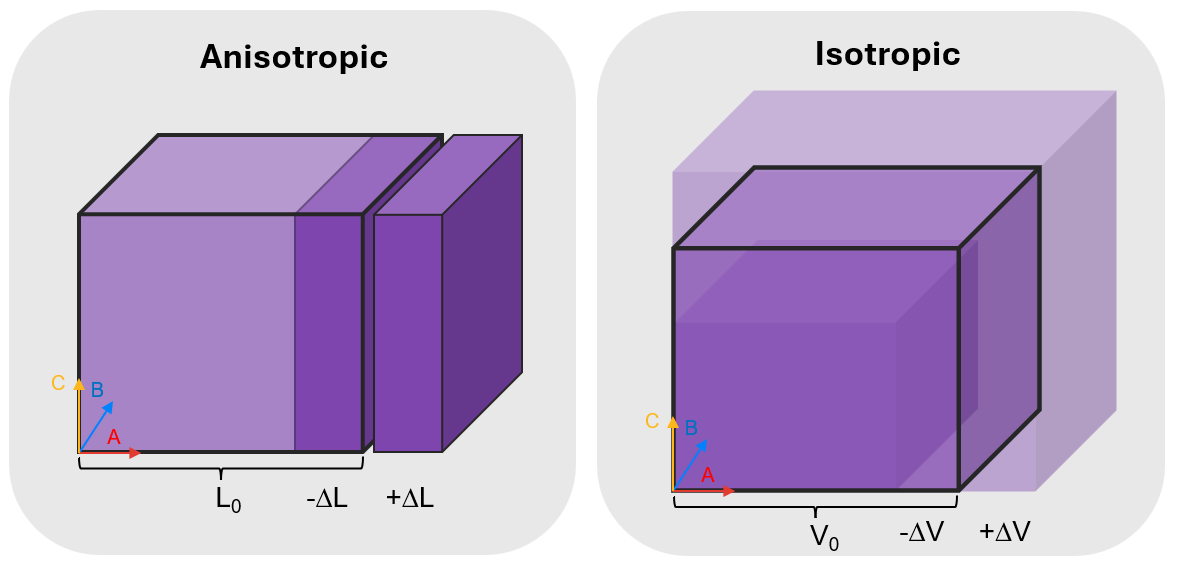
Fig. 178 Illustrative lattice vector expansion and contraction in the anisotropic and isotropic case.

A material property of interest is the temperature dependent macroscopic linear Grüneisen parameter(s), \(\gamma_L(T)\), which is determined from the microscopic quantities weighted by the heat capacities according to,

\[\gamma_L(T) = \frac {\sum_{i, \mathbf{q}} \gamma_L(\mathbf{q}, i) C_V(\mathbf{q}, i, T) w(\mathbf{q})} {C_V(T)}\]

where \(w(\mathbf{q})\) is the q-point weight determined from the phonon grid and the macroscopic heat capacity, \(C_V(T)\), is given by,

\[C_V(T) = \sum_{i, \mathbf{q}} C_V(\mathbf{q}, i, T) w(\mathbf{q})\]

For anisotropic materials, the Grüneisen parameter is a tensor with components for each direction, whereas for isotropic materials it reduces to a scalar value. Once the macroscopic Grüneisen parameter(s) are determined, the anisotropic linear and volumetric coefficients of thermal expansion are calculated according to [1],

\[\alpha_L(T) = \frac{C_V(T)}{V_0} \sum_{j\in{\{A,B,C\}}} S_{L,j} \gamma_j(T)\]

and

\[\alpha_V(T) = \sum_{j\in{\{A,B,C\}}} \alpha_{j}(T)\]

where \(S\) is the compliance tensor.

The isotropic linear and volumetric coefficients of thermal expansion are determined according to equations (17) and (18).

[1]

Gang “Liu, Jian Zhou, and Hui” Wang. “anisotropic thermal expansion of snse from first-principles calculations based on grüneisen’s theory”. “Phys. Chem. Chem. Phys.”, “19”:”15187–15193”, “2017”. URL: “http://dx.doi.org/10.1039/C7CP00815E”, doi:”10.1039/C7CP00815E”.