RadiusOfGyration¶

class RadiusOfGyration(md_trajectory, polymer_tags=None, start_time=None, end_time=None, time_resolution=None, mass_weight=None, gui_worker=None)¶

Analyzer to calculate the radius of gyration and shape factors of polymer chains.

Parameters:

md_trajectory (MDTrajectory | AtomicConfiguration) – The MDTrajectory or AtomicConfiguration that contains the polymers.
polymer_tags (list of type str | None | Automatic) – A list of tags for the polymers. If not specified default tags are used. Tags can also be set automatically with the flag Automatic
start_time (PhysicalQuantity of the type time) – The start time.
Default: 0.0 * fs.
end_time (PhysicalQuantity of the type time) – The end time.
Default: The last time image.
time_resolution (PhysicalQuantity of type time) – The time interval between snapshots in the MD trajectory that are included in the analysis.
Default: the MD time step.
mass_weight (bool) – Whether or not masses of atoms are included in the calculations.
Default: True.
gui_worker (PolymerAnalysisWorker) – Handle to the worker, for displaying the calculation progress.
Default: None.

acylindricalFactor()¶

Returns:: The acylindrical factor for each polymer chain. This is returned as a 2D array indexed by trajectory image then polymer chain.
Return type:: ndarray

anisotropicFactor()¶

Returns:: The anisotropic factor for each polymer chain. This is returned as a 2D array indexed by trajectory image then polymer chain.
Return type:: ndarray

asphericalFactor()¶

Returns:: The aspherical factor for each polymer chain. This is returned as a 2D array indexed by trajectory image then polymer chain.
Return type:: ndarray

components()¶

Returns:: The components of the radius of gyration. This is returned as a 3D array indexed by trajectory image, polymer chain, component.
Return type:: PhysicalQuantity of type length

polymerTags()¶

Return the polymer tags used for the analysis.

Returns:: A list of the polymer tags.
Return type:: list

radius()¶

Returns:: The radius of gyration of the polymers. This is returned as a 2D array indexed by trajectory image and then polymer chain.
Return type:: PhysicalQuantity of type length

times()¶

Returns:: Times for each image used in the analysis.
Return type:: PhysicalQuantity of type time

Usage Examples¶

Calculate the average radius of gyration of polystyrene chains during a molecular dynamics simulation starting from a well equilibrated configuration.

# -------------------------------------------------------------
# Initial Configuration
# -------------------------------------------------------------
bulk_configuration = nlread('Polystyrene.hdf5')[-1]

# -------------------------------------------------------------
# OPLS-AA Calculator
# -------------------------------------------------------------
potential_builder = OPLSPotentialBuilder()
calculator = potential_builder.createCalculator(bulk_configuration)
bulk_configuration.setCalculator(calculator)

# -------------------------------------------------------------
# Molecular Dynamics
# -------------------------------------------------------------
initial_velocity = ConfigurationVelocities(
    remove_center_of_mass_momentum=True
)

method = NPTMartynaTobiasKlein(
    time_step=1*femtoSecond,
    reservoir_temperature=300*Kelvin,
    reservoir_pressure=1*bar,
    thermostat_timescale=100*femtoSecond,
    barostat_timescale=500*femtoSecond,
    initial_velocity=initial_velocity,
    heating_rate=0*Kelvin/picoSecond,
)

constraints = [FixCenterOfMass()]

md_trajectory = MolecularDynamics(
    bulk_configuration,
    constraints=constraints,
    trajectory_filename='Polystyrene_Trajectory.hdf5',
    steps=100000,
    log_interval=10,
    trajectory_interval=1000,
    method=method
)

# -------------------------------------------------------------
# Calculate Radius Of Gyration
# -------------------------------------------------------------
analyzer = RadiusOfGyration(
    md_trajectory,
    start_time=0*ps,
    end_time=50*ps
)

radius_of_gyration = analyzer.radius()
radius_of_gyration_average = radius_of_gyration.mean(axis=1)
time = analyzer.times().convertTo(ps)

# -------------------------------------------------------------
# Plot The Results
# -------------------------------------------------------------
import pylab
pylab.figure()
pylab.plot(time, radius_of_gyration[:, 0], label='Polymer 1')
pylab.plot(time, radius_of_gyration[:, 5], label='Polymer 6')
pylab.plot(time, radius_of_gyration_average, label='Average')
pylab.xlabel('Time / ps')
pylab.ylabel('Radius Of Gyration / Angstrom')
pylab.legend()
pylab.savefig('Radius_Of_Gyration_Plot.png')

RadiusOfGyration_Example.py Polystyrene.hdf5

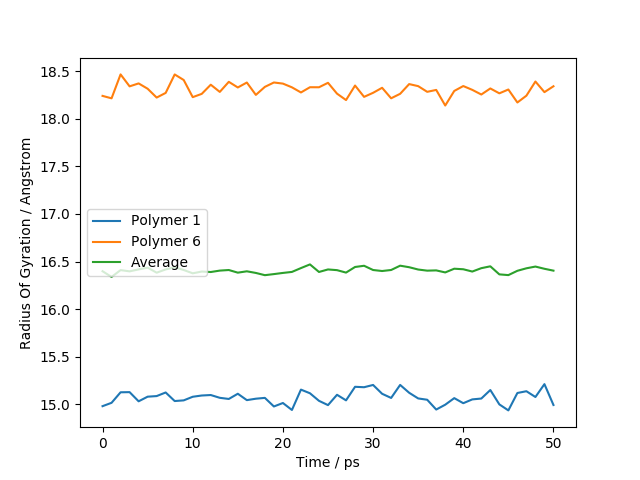
The script will run a short molecular dynamics calculation from the given starting structure and then calculate the radius of gyration for two individual polymers, as well as the average. This is shown in the following plot

../../../_images/Radius_Of_Gyration_Plot.png

Notes¶

This class enables the calculation of the radius of gyration and polymer chain shape descriptors from a MDTrajectory or BulkConfiguration[1]. The radius of gyration, \(R_g\) can be defined as:

\[R_g = \sqrt{\frac{\sum_i^N m_i(\mathbf{r}_i-\mathbf{r}_{COM})^2}{\sum_i^N m_i}}\]

Here \(m_i\) represents the mass of the atoms, \(\mathbf{r}_i\) represents the atomic positions and \(\mathbf{r}_{COM}\) represents the center of mass. As atomic masses are included, \(R_g\) defined here is the mass-weighted radius of gyration. Assuming each atomic mass is equivalent, produces the unweighted radius of gyration. The radius of gyration gives a measure of the overall size of the polymer chain.

Details about the shape can also be calculated. The principal components of the radius of gyration can be found by diagonalizing the gyration tensor. This gives three components \(\lambda_x\), \(\lambda_y\) and \(\lambda_z\) such that:

\[R_g^2 = \lambda_x^2 + \lambda_y^2 + \lambda_z^2\]

These components of the radius of gyration can give further information about the overall shape of the polymer chain. The asphericity of a polymer chain \(b\) measures the distance of the chain from a spherically symmetric shape, and is given as:

\[b = \lambda_x^2 - \frac{1}{2}\left(\lambda_y^2 + \lambda_z^2\right)\]

Similarly the acylindricity of the polymer chain \(c\) measures the deviation of the chain from a cylindrical shape. This can be defined as:

\[c = \lambda_y^2 - \lambda_z^2\]

Finally, the anisotropy of the polymer chain \(\kappa^2\) measures the amount to which the shape of the polymer is orientated is a particular direction. This can be defined as:

\[\kappa^2 = \frac{3}{2} \frac{\lambda_x^4+\lambda_y^4+\lambda_z^4}{(\lambda_x^2+\lambda_y^2+\lambda_z^2)^2} - \frac{1}{2}\]

To calculate each of these shape measures a RadiusOfGyration object first needs to be created. This takes a MDTrajectory or BulkConfiguration and calculates each of the size and shape measures for the specified configurations. The specific frames in the MDTrajectory to be analyzed can be selected using the start_time, end_time and time_resolution arguments. Whether or not mass weighting is used can be selected with the mass_weight argument. By default, mass weighting is used when calculating the radius of gyration. The polymer chains analyzed in the configuration can be specified with the polymer_tags argument. This takes a list of tags of polymer molecules in the configuration. By default polymers tagged with POLYMER_MOLECULE_# are analyzed, where # is a numerical index. These tags are added automatically to polymer configurations built with the PolymerMonteCarloBuilder, or can be added using the function tagPolymerMolecules()

Once the RadiusOfGyration object is created and the values of each of the descriptors has been calculated, the values can be queried using the remaining methods. Each of these returns arrays of values indexed first by the trajectory frame, then by the polymer. Averaging over all frames can be done by averaging over axis 0, while averaging over polymer chains is achieved by averaging over axis 1.