Viscosity¶

class Viscosity(md_trajectories, start_time=None, end_time=None, measurement_name='pressure_tensor', info_panel=None)¶

Class for calculating the shear viscosity from an MDTrajectory.

Parameters:

md_trajectories (MDTrajectory | list of type MDTrajectory) – The MDTrajectory the viscosity should be calculated for. This may be given as a single MDTrajectory or as a list of MDTrajectory objects.
start_time (PhysicalQuantity of type time) – The start time.
Default: 0.0 * fs
end_time (PhysicalQuantity of type time) – The end time.
Default: The last frame time.
measurement_name (str) – The name of the measurement in the MDTrajectory that contains the pressure tensor data.
info_panel (InfoPanel (Plot2D)) – Info panel to show the calculation progress.
Default: No info panel

correlationFunction()¶

Returns:: The shear pressure autocorrelation function.
Return type:: PhysicalQuantity of type pressure**2

lagTimes()¶

Returns:: The lag times of the shear pressure autocorrelation function.
Return type:: PhysicalQuantity of type time

temperature()¶

Returns:: The temperature of the MD simulation.
Return type:: PhysicalQuantity of type temperature

uniqueString()¶: Return a unique string representing the state of the object.

viscosities()¶

Returns:: An estimate of the viscosity using the Green-Kubo formalism as a function of lag time.
Return type:: PhysicalQuantity of type time * pressure

viscositiesStandardError()¶

Returns:: The standard error of the mean for the estimated viscosity.
Return type:: PhysicalQuantity of type time * pressure

Usage Examples¶

This example runs a NVT molecular dynamics (MD) simulation of a Lennard-Jones fluid. The pressure tensor is recorded at each MD step, using the MDMeasurement measurement hook.

initial_velocity = MaxwellBoltzmannDistribution(
    temperature=T,
    enforce_temperature=True,
    remove_center_of_mass_momentum=True
)

method = NVTNoseHoover(
    time_step=10.0*femtoSecond,
    initial_velocity=initial_velocity,
    thermostat_timescale=1*ps,
    reservoir_temperature=T,
)
constraints = [FixCenterOfMass()]

measurement_names = ['pressure_tensor']

md_trajectory = MolecularDynamics(
    bulk_configuration,
    constraints=constraints,
    trajectory_filename='ljmd.hdf5',
    steps=100000,
    log_interval=1000,
    measurement_hook=MDMeasurement(measurement_names, call_interval=1),
    method=method
)

The shear viscosity is then calculated from the MD trajectory.

viscosity = Viscosity(
    md_trajectory,
    start_time=10*ps,
    measurement_name='pressure_tensor',
)
nlsave('viscosity.hdf5', viscosity)

The script will produce a plot of the estimated viscosity as a function of the maximum lag time as well as a reference value taken from [1].

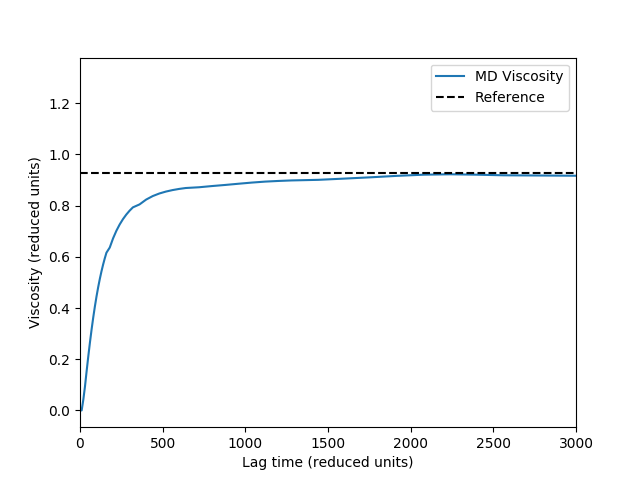
Notes¶

The viscosity is calculated from the shear pressure using the Green-Kubo relations. [2] In the Green-Kubo formalism, the viscosity is defined as,

\[\eta = \frac{V}{k_\mathrm{B}T} \int_0^\infty \langle P_{\alpha\beta}(\tau_0)P_{\alpha\beta}(\tau_0 + \tau) \rangle \mathrm{d}\tau,\]

where \(V\) is the volume of the unit cell, \(k_\mathrm{B}\) is the Boltzmann constant, \(T\) is the temperature, \(P\) is the pressure tensor with \(P_{\alpha\beta}\) indicating the off-diagonal elements (shear), the angle brackets represent an ensemble average over trajectories with time origin \(\tau_0\), and \(\tau\) is the lag time between two pressure tensors. In practice the MD simulations will be of finite length and the integral must be truncated at finite time.

As the pressure tensor needs to be recorded with a high frequency (ideally every MD time step) and the trajectories are often on the time scale of 1 ns, the multiple-tau correlation technique is used to calculate the shear pressure autocorrelation function. [3]
This analysis class is designed to be used with the MDMeasurement hook function. This allows for the pressure tensor to be recorded at each time step, without saving the full configuration to the MDTrajectory.
The analysis class can analyze a single trajectory or a list of multiple trajectories. If multiple trajectories are given, then it is assumed that each trajectory is independent. Additionally, the standard error of the estimated viscosity, as a function of lag time, can be obtained by calling viscositiesStandardError.